Понятие кусочно-гладкой пространственной кривой. Определение криволинейного интеграла по длине дуги (=1-го рода) и его вычисление. Понятие ориентированной кусочно-гладкой пространственной кривой. Определение криволинейного интеграла по координатам, механический смысл и основные свойства. Вычисление криволинейных интегралов по координатам, страница 2

Если на плоскости Оху взят контур Г: , то получим

30.Теорема Грина о связи криволинейного интеграла по координатам от функции двух переменных с соответствующим двойным интегралом.

Пусть D правильная область в плоскости Оху, ограниченная контуром Г. Пусть в D определены функции Р(х,у) и Q(х,у), непрерывные вместе с частными производными  и . Тогда справедлива формула Грина .

Доказательство: Будем считать, что Г состоит из дуги ,  и двух прямолинейных отрезков MR и SN параллельных оси Оу.

Тогда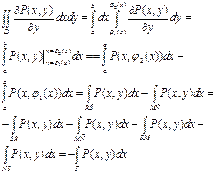

Получили .

Рассматривая область D правильной в направлении оси Ох, проводя те же рассуждения получим .  (2)+(3) = (1).

Замечание: Формула Грина остается в силе, если вместо правильной области D рассматривать любую область, которую можно разбить на конечное число правильных областей.

Следствие: Пусть , тогда площадь области D  . А если , то .

31. Условия независимости криволинейного интеграла по координатам от формы питии интегрирования.

Теорема: Следующие 4 утверждения равносильны (при условии, что выполняется условие теоремы Грина).

1. В каждой точке области D .

2. Для любого замкнутого контура Г, лежащего в D интеграл .

3. Выражение Pdx+Qdy является полным дифференциалом некоторой функции u(x,y), имеющий непрерывную частную производную первого порядка u_x’и u_y’, т.е.  Pdx+Qdy=du, тогда P=дu/дх, Q= дu/дy. (утверждение 3 вытекает из 2 в силу интегрируемости выражения Pdx+Qdy).

4. не зависит от формы пути  идущего в D из А в В, а зависит лишь от начала пути А и конца пути В. Причём  - аналог формулы Ньютона-Лейбница. (следует из 3). (Из 3 следует 2 в силу равенства смешанной производной для непрерывной функции).

32. Понятие гладкой и кусочно-гладкой поверхности. Интегральные суммы для функции трех переменных по кусочно-гладкой поверхности. Определение и важнейшие свойства поверхностного интеграла 1-го рода.

Поверхность π в пространстве Oxyz называются гладкой, если в каждой её точке существует касательная плоскость, причём при переходе от точки к точке эта касательная плоскость меняется непрерывно. Поверхность π называется кусочно-гладкой если ее можно разбить на конечное число гладких частей. Пусть в пространстве Охуz задана кусочно-гладкая поверхность π и на ней определена ограниченная функция  f(x,y,z)=f(M). Разобьем  π произвольно на n частей π₁,π₂,…,π_n. Пусть ΔS₁,ΔS₂,…,ΔS_n - площади частей  π₁,π₂,…,π_n.. Полученное разбиение обозначим  τ и назовем рангом разбиения λ=λ_τ - наибольший из диаметров частей π₁,π₂,…,π_n. На каждой части π_k выберем произвольно точку M_k(x_k,y_k,z_k) - промежуточные точки разбиения τ.

Составим сумму

 (1).

(1) называется интегральной суммой, отвечающей данному разбиению τ и данному выбору промежуточных точек.

, где D_k - диаметр всех плоскостей π_k.

Опр: Число I называют конечным пределом интегральных сумм (1) и пишут , если для любого ε>0 найдется  δ>0 такое, что при любом разбиении τ поверхности π на части π₁,π₂,…,π_n., удовлетворяющее условию λ<δ, и любом выборе промежуточных точек M_k выполняется неравенство |I–σ|<ε.

Опр: Если существует конечный предел интегральных сумм (1) при λ→0, то он называется поверхностным интегралом от функции f(x,y,z) по площади поверхности π или поверхностным интегралом первого рода по поверхности π и обозначают символом . При этом функция f(x,y,z) называется интегрируемой по площади поверхности π.

Поверхностные интегралы первого рода вводятся также как обычные двойные интегралы, поэтому все основные свойства двойных интегралов переносятся и на поверхностные интегралы первого рода. В частности:

1.  площадь поверхности π.

2. Теорема о среднем значении: Если функция  f(x,y,z) непрерывна на поверхности π, то существует точка  такая, что .

Механический смысл поверхностных интегралов.