Министерства образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра
Радиоприемная и радиопередающая кафедра
Расчетно-графическое задание
по теории управления и радиоавтоматике
Выполнил студент факультета РЭФ
группы РТ5-03
Панарин А.С.
Проверил преподаватель
Лявданский С.Е.
Новосибирск
2003 г.
Задано:
Передаточная функция замкнутой системы:
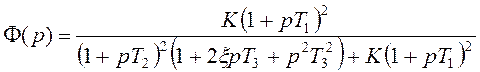

Выполнить следующее:
1. Записать передаточную функцию разомкнутой системы K(p).
2. Зарисовать структурную схему системы считая ее следящей. Перечислить все типовые структурные звенья в системе.
3. Записать передаточную функцию и дифференциальное уравнение замкнутой системы.
4. Записать передаточную функцию для ошибки от регулирующего воздействия.
5. Записать характеристические полиномы замкнутой и разомкнутой системы и вычислить их коэффициенты.
6. Произвести анализ устойчивости по критерию Гурвица.
7. Произвести анализ устойчивости по критерию Михайлова (метод чередующихся корней). Построить годограф Михайлова.
8. Произвести анализ устойчивости по критерию Найквиста. Построить годограф Найквиста. Определить запас системы по фазе и по модулю.
9.
Определить ошибку регулирования ![]() (t) и построить график.
(t) и построить график.
Решение.
1. Передаточная функция разомкнутой системы. Нам известна передаточная функция замкнутой системы:
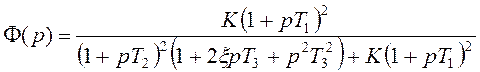
Но нам еще известно, что тот же коэффициент передачи замкнутой системы связаны между собой следующим соотношением:
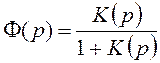
тогда сделаем следующую операцию:
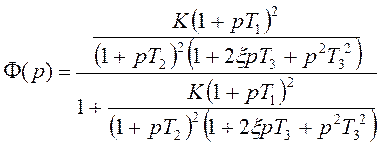
Тогда из данных операций следует, что коэффициент передачи разомкнутой системы будет следующее выражение:
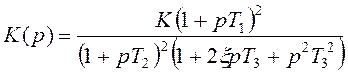
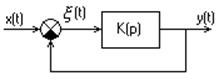
2. Структурная схема системы(система считается следящей. И перечисление всех типовых звеньев в системе.
Следящая система выглядит следующим образом простейшая ее структура выглядит следующим образом:
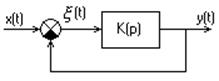
Зная коэффициент передачи разомкнутой системы
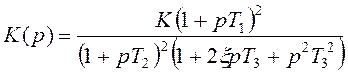
Можно сказать, что коэффициент передачи разомкнутой системы можно разложить на несколько составляющих:
![]()
где
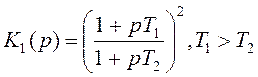 , то есть это означает что это звено есть
упруго дифференцирующее второго порядка.
, то есть это означает что это звено есть
упруго дифференцирующее второго порядка.
У нас еще остался коэффициент К2(p):
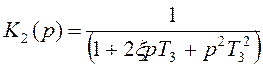
Это есть колебательное звено.
Структурная схема выглядит тогда так:
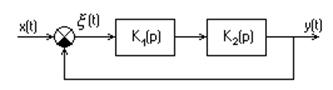
3. Передаточная функция и дифференциальное уравнение замкнутой системы.
Передаточная функция замкнутой системы:
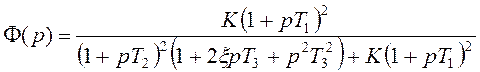
Передаточную функцию замкнутой системы можно записать следующим образом:
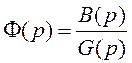
где B(p) – характеристический полином
G(p) – характеристический полином замкнутой системы.
тогда можно записать следующее выражение:
Характеристический полином замкнутой системы по определению равняется характеристический полином разомкнутой системы плюс характеристический полином B(p), то есть G(p) = A(p) + B(p).
Тогда соответственно распишем характеристические полиномы A(p) и B(p):
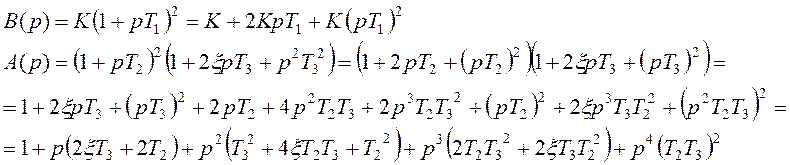
Тогда дифференциальное уравнение замкнутой системы будет выглядеть следующим образом:
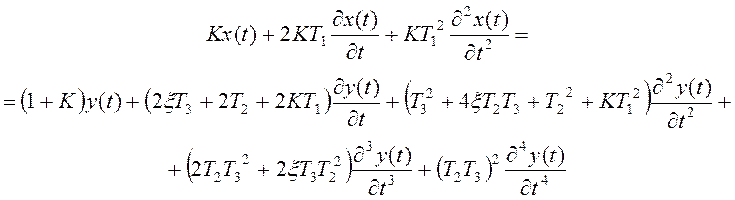
4. Передаточная функция для ошибки от регулирующего воздействия
Известно, что передаточная функция для ошибки от регулирующего воздействия:
![]()
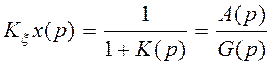
где
 Передаточная
функция для ошибки от регулирующего воздействия
Передаточная
функция для ошибки от регулирующего воздействия
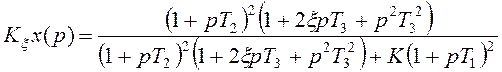
5. Характеристические полиномы замкнутой и разомкнутой системы. Вычисление их коэффициентов.
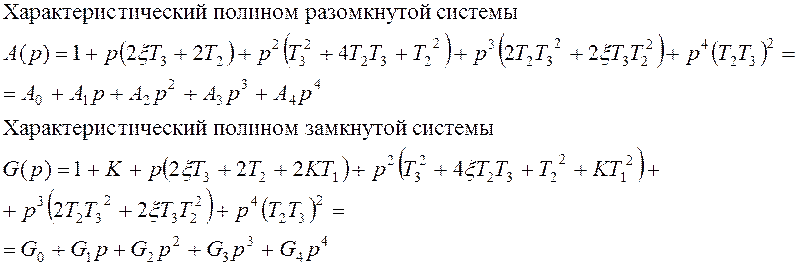 Вычисление
коэффициентов характеристического полинома замкнутой системы:
Вычисление
коэффициентов характеристического полинома замкнутой системы: 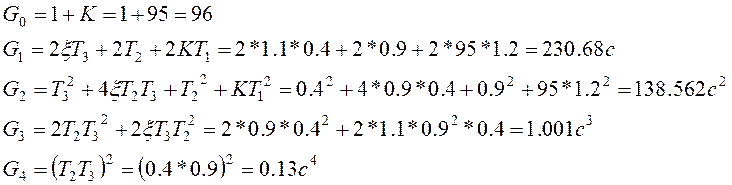
![]()
Вычисление коэффициентов характеристического полинома разомкнутой системы:
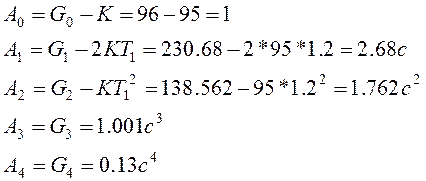
![]()
6. Анализ устойчивости системы по критерию Гурвица.
Анализ устойчивости системы по критерию Гурвица разомкнутой системы:
Известно характеристический полином разомкнутой системы:
![]()
где соответственно коэффициенты можно обозначить как
![]()
Так как коэффициенты характеристического полинома все больше нуля, то необходимое условие устойчивости критерия Гурвица выполняется, тогда проверяем на устойчивость разомкнутой системы по достаточному критерию Гурвица.
Запишем матрицу:
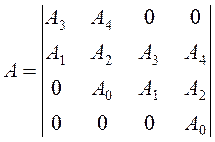
Достаточное условие устойчивости – положительные значения всех диагональных определителей:
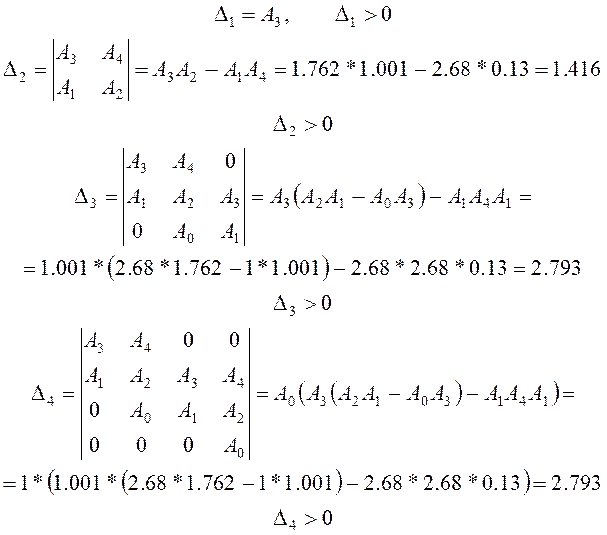
Достаточное условие было выполнено то есть система устойчива.
Разомкнутая система устойчива.
Анализ устойчивости системы по критерию Гурвица замкнутой системы:
Известно характеристический полином замкнутой системы:
![]()
где соответственно коэффициенты можно обозначить как
![]()
Так как коэффициенты характеристического полинома все больше нуля, то необходимое условие устойчивости критерия Гурвица выполняется, тогда проверяем на устойчивость разомкнутой системы по достаточному критерию Гурвица.
Запишем матрицу:
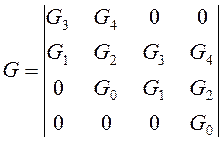
Достаточное условие устойчивости – положительные значения всех диагональных определителей:
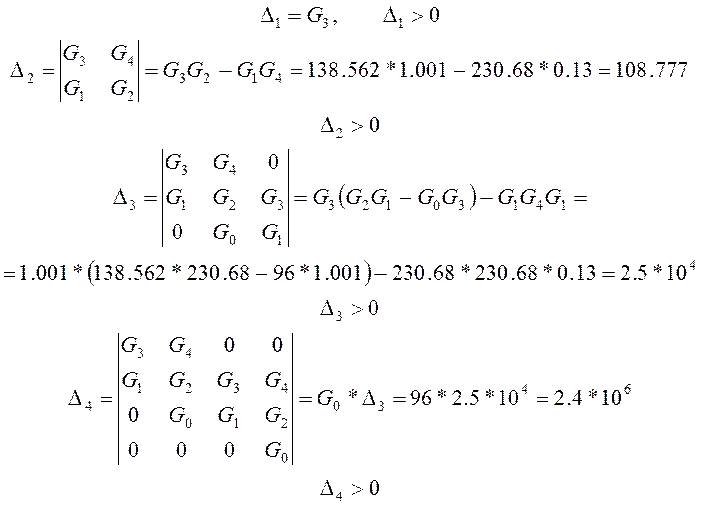
Достаточное условие было выполнено то есть система устойчива.
Замкнутая система устойчива.
7. Анализ устойчивости с помощью критерия Михайлова(метод чередующихся корней) Построение годографа Михайлова. Запишем характеристический полином замкнутой системы:
![]()
Перейдем в частотную область:
![]()
Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.
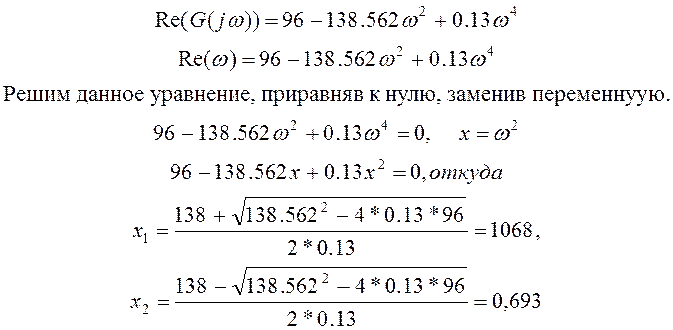
Взяв только положительное значение частот, получим
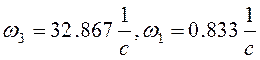
Находим частоты пересечения вещественной оси приравняв к нулю мнимую часть:
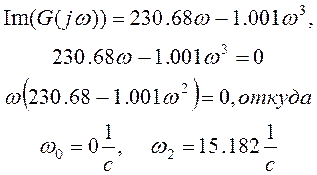
Расположим корни нашего уравнении одни возле другого последовательно по возрастанию.
0, 0.833, 15.182, 32.867
Так как корни одного уравнении, не расположены друг возле друга то система устойчива.
Начертим годограф по критерию Михайлова:
Составим таблицу значений:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.