Общие сведения о нелинейных цепях и методах их исследования, страница 4

В теории радиотехнических цепей (и вообще в радиотехнике) для аппроксимации характеристик НЭ наиболее часто используют следующие функции.

      3.1. Степенной полином:

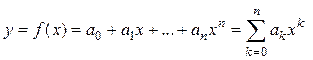                                  ,                                         (1.6)

где

.

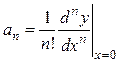В соответствии с точечным приближением (методом выбранных точек) получаем систему уравнений:

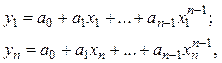                                                                             (1.7)

решение которой и позволит найти коэффициенты .

Для окрестности с рабочей точкой  полином (1.6) можно записать в виде ряда Тейлора

 =

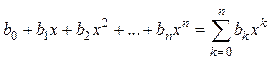                         = ,                                            (1.8)

где

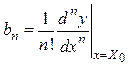.                                                 (1.9)

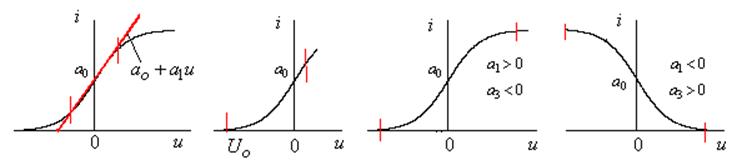
Полиномом первой степени аппроксимируют линейные участки характеристик НЭ только при изучении линейных явлений (рис.1.9,а). Параболу используют для аппроксимации начальных участков характеристик НЭ при действии малых входных сигналов (рис.1.9.б). Укороченный полином третьей степени (без члена ) применяют в том случае, если надо передать замедление роста функции (усилительных свойств НЭ) с увеличением входного сигнала (рис.1.9,в,г)

а)                                  б)                             в)                                  г)

Рис. 1.9

Обычно , при этом в ряде случаев характеристика может содержать только четную или только нечетную часть.

Четные и нечетные части характеристик. Следует отметить, что любую нелинейную характеристику можно представить в виде суммы четной и нечетной функций

.                                   (1.10)

Четная и нечетная функции удовлетворяют выражениям:

.                                                   =, .                          (1.11)

Из (1.10) с учетом (1.11) получаем

                                                           ,                                    (1.12)

Складывая и вычитая выражения (1.10) и (1.12), получаем

                      ,  .                    (1.13)

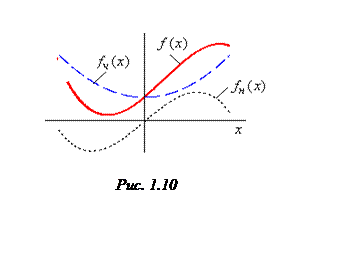
На рис.1.10 дан пример функции , её четной  и нечетной  составляющих.

При степенной аппроксимации характеристик НЭ ее четная и нечетная части складываются из четных и нечетных степеней:

        .                  (1.14)

Целесообразность выделения четной и нечетной частей характеристик обусловлена рядом причин. Во-первых, наличие таких характеристик  во многих случаях облегчает понимание физической сущности процессов в анализируемой цепи. Во-вторых, работа многих преобразователей сигналов определяется только четной (модуляция, детектирование), или нечетной (усиление, генерирование) частью характеристики. Кроме того, по виду этих характеристик можно судить о минимальной  степени полинома, правильно описывающем их основные особенности.  Вид четной и нечетной части характеристики дает возможность оценить «на глаз» применимость данного НЭ для осуществления требуемого преобразования сигнала.

Согласно выражений (1.11) можно получить схемные решения для четной и нечетной характеристик нелинейных цепей. Для этого нужно использовать два идентичных НЭ, работающих в одинаковых режимах. Переменные напряжения на их входы должны подаваться в противофазе, что реализуется с помощью трансформатора, как показано на рис.1.11, а и б. Для формирования четной части характеристики требуемое выходное напряжение следует снимать с сопротивления нагрузки , где протекает сумма токов  (рис.1.11,а); при этом . В схеме рис.1.11,б формирования нечетной части характеристики  нагрузка включена  так, что выходное напряжение пропорционально разности токов . Тогда , то есть пропорционально .

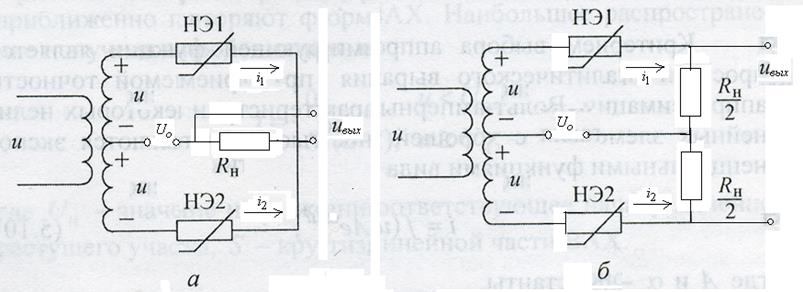
Рис. 1.11

3.2. Экспоненциальный полином:

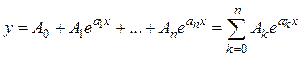.                                                     (1.15)

Этим полиномом можно достаточно точно описать любую характеристику НЭ. В общих чертах внутренние процессы в НЭ подчиняются законам пропорционального роста, когда скорость изменения функции пропорциональна самой функции.

В ряде случаев используют лишь одну экспоненту. Например, характеристика вакуумного диода представляется выражением

.                                       (1.16)

Коэффициент  определяется из условия: при , . Для определения коэффициента  можно воспользоваться методом выбранных точек, то есть задать точку совпадения () заданной и аппроксимирующей функций: . Тогда .