Классификация автоматических систем. Методы анализа линейных систем радиоавтоматики. Характеристики линейных систем радиоавтоматики, связь между ними, страница 3

ПФ ошибки от регулирующего воздействия:

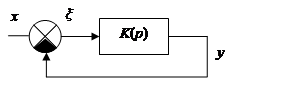
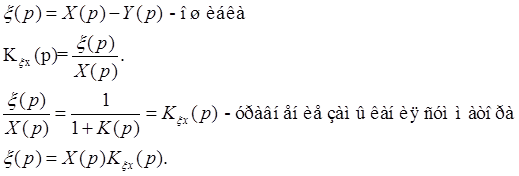
ПФ от регулирующего воздействия одинакова как для следящей, так и для не следящей системы.

ПФ ошибки от возмущающего воздействия:

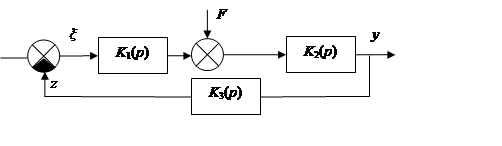
F ≠ 0, x ≠ 0.

F – возмущающее воздействие, помеха K_ξF.

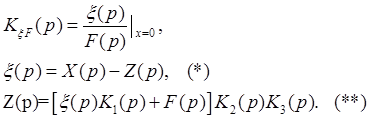
Подставляем (**) в (*) при x = 0:

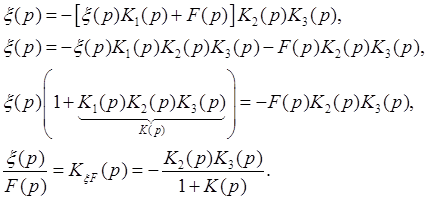
Передаточная функция ошибки возмущающего воздействия есть отношение, где в числителе со знаком минус взята передаточная функция части системы, находящейся между точкой приложения возмущающего воздействия и сумматором (по ходу сигнала).

Поскольку система линейная, соблюдается принцип суперпозиции (независимость прохождения сигналов друг от друга):

.

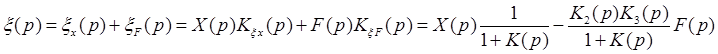Вопрос 9

Устойчивость линейных САУ. Теорема Ляпунова. Критерий Гурвица

Устойчивость – свойство системы возвращаться в условие равновесия после снятия внешних сил, выведших её из состояния равновесия.

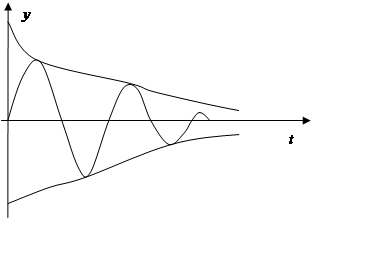
Траектория описывается уравнением

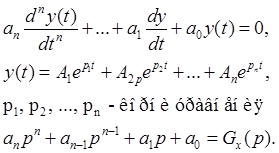
Самыми распространёнными критериями определения устойчивости системы являются алгебраический критерий Гурвица, частотные критерии Найквиста и Михайлова.

Теорема Ляпунова:

Если в характеристическом полиноме системы нет корней с положительными или нулевыми вещественными частями, то такая система будет устойчива.

Критерий Гурвица:

Необходимое условие устойчивости:

Все коэффициенты характеристического полинома системы должны быть положительны:

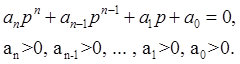
Тогда все корни данного уравнения будут иметь отрицательные вещественные части.

Достаточное условие устойчивости

Все диагональные определители матрицы должны быть положительны.

Матрица размера nx n (n – максимальная степень полинома).

По диагонали сверху вниз вписываются коэффициенты от a_n-1 до a₀, остальные по возрастанию вправо, по убыванию влево, и нули.

Например, если полином 4-й степени, то матрица будет иметь вид:

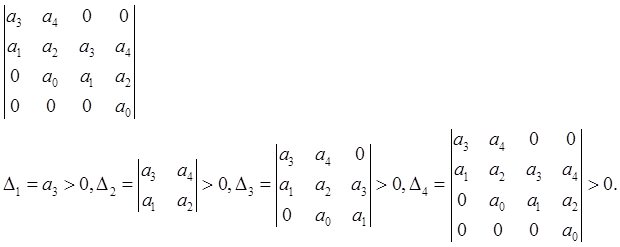
Вопрос 10

Частотный критерий Найквиста. Примеры

Частотный критерия Найквиста позволяет определить, какими параметрами устойчивости обладает данная система.

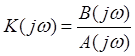,     - характеристическая функция разомкнутой системы.

.

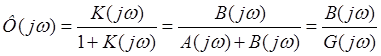 - характеристическая частотная функция замкнутой системы.

Передаточная функция ошибки:

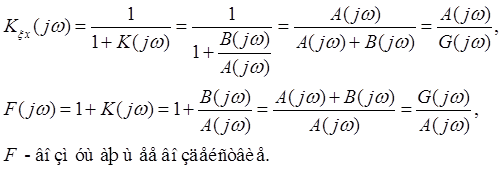
Рассмотрим 2 возможные ситуации:

I. Разомкнутая система устойчива. Найдём условие, при котором замкнутая система тоже будет устойчива.

A(p) = 0 – характеристическое уравнение разомкнутой системы.

- корни.

.

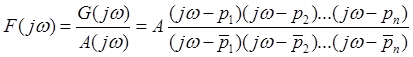Фазовый набег:  

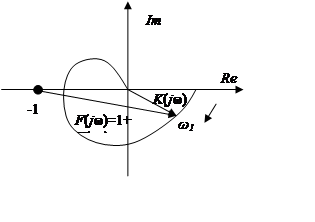Если разомкнутая система устойчива, то замкнутая система может быть устойчива, если годограф функции K(jω) разомкнутой системы в диапазоне частот от 0 до ∞ не охватывает точку (-1, 0) на вещественной оси.

Примеры:

Статическая система

K₁ < K₃ < K₂, K₃ – критический коэффициент усиления.

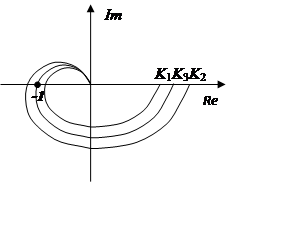
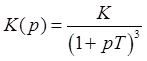.                             Астатическая система

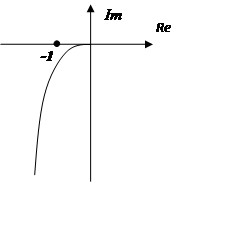
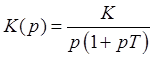 - интегрирующее звено сразу даёт сдвиг 90°. Эта система структурно устойчива.

Система структурно не устойчива с двойным интегрирующим звеном:

.

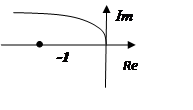
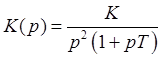Вопрос 11

II. Разомкнутая система неустойчива, а замкнутая система будет устойчивая.

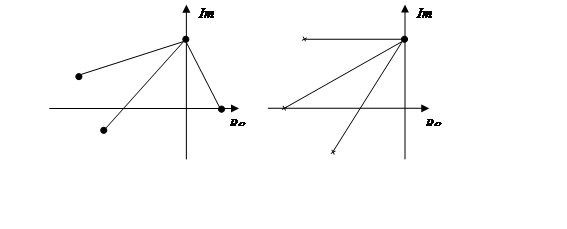
Пусть в уравнении A(p)=0 из n корней m в правой полуплоскости:

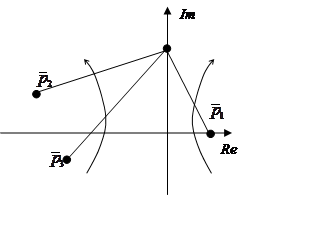
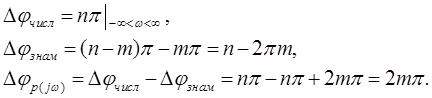
Если разомкнутая система неустойчива и её характеристическое уравнение A(p)=0 имеет m корней с положительной вещественной частью, то для устойчивости замкнутой системы фазовый набег вектора F(jω) должен составлять m/2 полных оборота (годограф K(jω) в диапазоне частот от 0 до ∞ m/2 раз против часовой стрелки охватывает точку (-1,0)).

Пример:

Если m=2, то годограф для устойчивого состояния должен 1 раз охватить точку (-1,0).

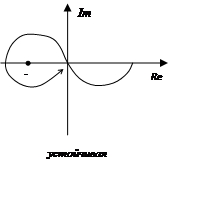
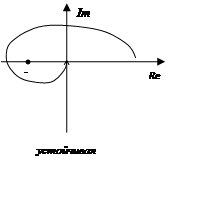
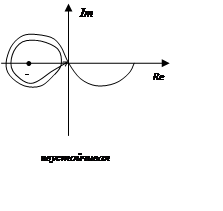
m=3:

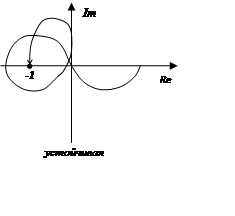
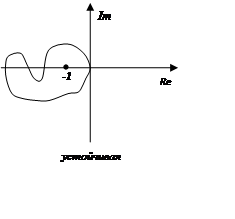
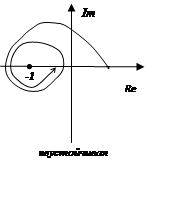
Вопрос 12

Частотный критерий Михайлова. Примеры

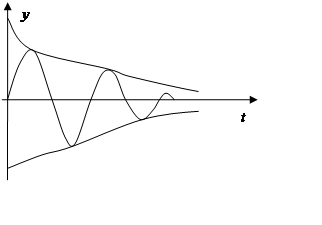
Траектория описывается уравнением

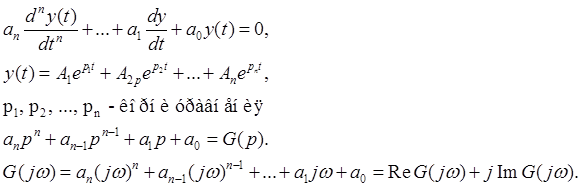
Все корни должны быть в левой полплоскости:

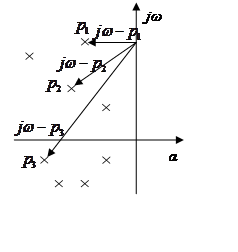
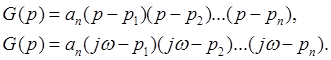
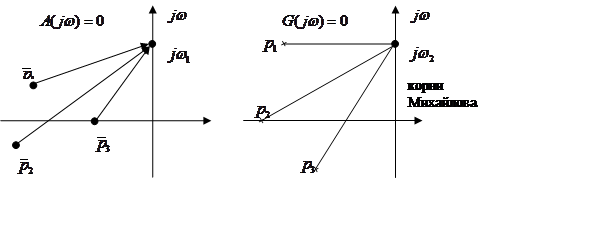
Фазовый набег вектора G(jω):

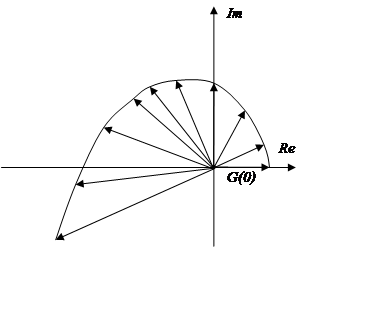
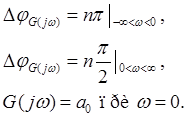
- Годограф характеристической частотной функции замкнутой системы (годограф Михайлова)

Частотный критерий Михайлова:

Замкнутая система будет устойчива, если годограф характеристической частотной функции замкнутой системы при изменении частоты от 0 до ∞, начинаясь с вещественной оси, последовательно, против часовой стрелки, обходит n квадрантов и в последнем квадранте уходит в бесконечность.