Методические указания к выполнению лабораторного практикума по дисциплине «Радиоавтоматика», страница 5

«Краеугольным камнем» теории устойчивости системы автоматического регулирования  является теорема А.М. Ляпунова, согласно которой замкнутая система будет устойчивой, если все корни характеристического уравнения замкнутой системы имеют отрицательные вещественные части. Получить характеристическое уравнение очень просто: характеристический полином замкнутой системы (знаменатель передаточной функции) приравнивается нулю. Конечно, решать подобные алгебраические уравнения, особенно высоких порядков, непросто. Поэтому постепенно стали появляться критерии устойчивости (Гурвица, Найквиста, Михайлова). В данной работе активно задействованы критерии А.В. Михайлова и Г. Найквиста. Оба эти критерия являются частотными, так как рассматривают поведение на комплексной плоскости годографов неких частотных функций исследуемой системы. В частности, критерий Найквиста рассматривает форму годографа комплексного коэффициента передачи разомкнутой системы . Формулируется критерий Найквиста так: 

- если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо, чтобы годограф функции  в диапазоне частот от нуля до бесконечности не охватывал точку -1 на вещественной оси.

-  если же разомкнутая система неустойчива (значит, по А.М. Ляпунову, в её характеристическом уравнении есть корни с положительной вещественной частью), то для устойчивости замкнутой системы необходимо, чтобы годограф  охватывал точку -1, причем против часовой стрелки, да ещё и строго определенное число раз. В частности, если количество корней с положительной вещественной частью в характеристическом уравнении разомкнутой системы обозначит буквой m, (именно поэтому она и неустойчива по Ляпунову), то количество охватов годографом точки -1 должно быть равно m/2.

      Критерий Михайлова рассматривает годограф характеристической частотной функции G(ιω) на комплексной плоскости и формулируется следующим образом: годограф характеристической частотной функции замкнутой системы G(ιω), начинаясь на вещественной оси, должен последовательно против часовой стрелки обойти столько квадрантов комплексной плоскости, каков порядок характеристического полинома. Характеристическая частотная функция замкнутой системы – это знаменатель передаточной функции замкнутой системы, в котором индекс комплексной частоты р заменён на ίω. Более подробно оба частотные критерия устойчивости рассмотрены в методическом пособии [1], стр. 10-19.

Список контрольных вопросов

1.  Как изменится форма годографа Найквиста, если в систему №1 вместо упругого дифференцирующего звена последовательной коррекции ввести звено реальное дифференцирующее?

2.  Как изменится форма годографа Найквиста, если в систему №1 вместо упругого дифференцирующего звена последовательной коррекции ввести форсирующее?

3.  Как изменится форма годографа Найквиста, если в систему №1 вместо упругого дифференцирующего звена последовательной коррекции ввести интегрирующее?

4.  Как изменится форма годографа Найквиста, если в систему №1 вместо упругого дифференцирующего звена последовательной коррекции ввести  инерционное?

5.  Структура системы: 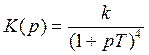                                       K< Kкр

Как выглядят годографы Найквиста и Михайлова?

6.   Структура системы: 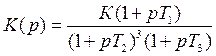          K>Kкр

Как выглядят годографы Найквиста и Михайлова?

7.  Структура системы: 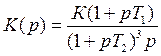              K< Kкр

Как выглядят годографы Найквиста и Михайлова?

8.  Структура системы: 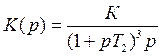                                  K< Kкр

Как выглядят годографы Найквиста и Михайлова?

9.  Структура системы: 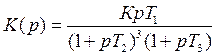         K>Kкр

Как выглядят годографы Найквиста и Михайлова?

10.  Структура системы: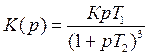

Как выглядят годографы Найквиста и Михайлова?

11.  Структура системы: 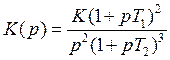            K>Kкр

Как выглядят годографы Найквиста и Михайлова?

12.  Структура системы: 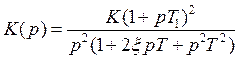            T1 >T

Как выглядят годографы Найквиста и Михайлова?

13.  Структура системы: 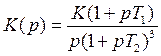                             K>Kкр