Другие предметы \ Антенны и устройства СВЧ

Метод наводимых электродвижущих сил, страница 6

Далее находятся остальные составляющие векторных напряженностей электромагнитного поля в ближней зоне, а именно нормальная составляющая ER и тангенциальная составляющая Нф (напоминание: используется цилиндрическая система координат R,pp,z). Из первого уравнения Максвелла в цилиндрических координатах имеем:


RHjC£0srEz =

jC£0£rER


1 d

R dR L

-dHpp dz


p

> 


Записывая (1.35) в виде


Ez


WI0

jkR1 *

4;rkl sin kl R dR   R1*


-jkR2*               e-jkR0*

--------- 2cos kl---------- ]

R2*                   R0*


(1.38)


и сравнивая с (1.37), получаем с учетом <jos0sr/k=1/W:


Hp =


e

jkRx *

4;rR sin kl    R1*


■ + --------- 2cos kl---------- ].

R2*                 R0*


(1.39)


Подставляя теперь (1.39) в выражение для ER из (1.37), находим:


jkRi

Er


e

jWI0

4nR sin kl   R1*


■( z -1) +


-jkRi

R2


(z +1) - 2cos kl


e~jkR0* R0*

(1.40)


Расчеты показывают, что для диполя, радиус которого стремится к нулю (а—-0), составляющая ER(p=a) на поверхности диполя согласно (1.40) стремиться к бесконечности, в то время как Ez(z,p=a) в соответствии с формулой (1.35) остается везде, за исключением концов диполя, конечной. Это означает, что электрические силовые линии подходят к оси диполя почти под прямым углом [tg(ER/Ez)—oo], как это и должно быть в действительной картине ближнего поля на боковой цилиндрической поверхности диполя определяет ток проводимости на диполе, а нормальная составляющая электрического поля на боковой поверхности определяет собой линейную плотность заряда Qz(z) вдоль диполя, что следует из уравнений:


Iz (z) = 2naHp (p = a),  Qz (z) = 2nas0SrER (p = a),


(1.41)


где Нф(р=а) и ER(p=а) - есть напряженности магнитного и электрического полей на поверхности диполя в точке (точнее: сечении) с координатой z. Из последних


двух уравнений (1.41) также вытекает, что для заданной величины тока I0 на входных клеммах диполя (а, следовательно, и заряда) напряженность магнитного поля вокруг диполя и нормальная составляющая векторной напряженности электрического поля на поверхности диполя тем больше, чем меньше радиус а диполя.

Теперь можно приступить к расчету мощности излучения диполя, взяв в качестве замкнутой поверхности интегрирования цилиндр с высотой 2L и радиусом р. В центре этого цилиндра вдоль его оси расположим диполь (рис. 1.5). Нормальные составляющие вектора Пойнтинга в цилиндрической системе координат имеют выражения:

PR =-2Ez(z)Hp *(z), Pz = 2Er(z)Hp *(z),                                          (1.42)

где «звездочка» означает в данном случае комплексную сопряженность. Ясно, что интеграл



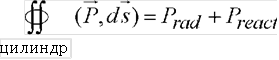(1.43)


по поверхности цилиндра определяет мощность, подводимую к диполю и излучаемую им. При этом, так как вектор Е и вектор Н не находятся в ближней зоне в фазе, то мощность (1.43) получается комплексной, т.е. имеет как активную составляющую Prad (она характеризует излучаемую энергию в единицу времени, уходящую от диполя в безграничное пространство), так и реактивную Preact (она характеризует колебательный процесс обмена реактивной мощности между диполем и ближним электромагнитным полем).

Совместим рассматриваемую поверхность цилиндра с поверхностью диполя [другими словами: «натянем» поверхность интегрирования в (1.43) на диполь как чулок], т.е. положим р=а, L=l. Тогда при неограниченном уменьшении радиуса а поверхностные интегралы в (1.43) по верхнему и нижнему основаниям цилиндра будут стремиться к нулю и мощность Ps определиться интегрированием только по боковой поверхности цилиндра (диполя):

z=l р=2ж

Ps= 2 JJ  PRadzdp.                                                                                                                   (1.44)

z=0 p=0

Здесь взят удвоенный интеграл, так как вследствие симметрии относительно центра диполя интегрирование ведется по одной половине цилиндра от z=0 до z=l. Подставляя в (1.44) выражение PR из (1.42) и учитывая, что ближнее поле от координаты p не зависит, получаем:

z=l

Ps = - J Ez (z, p = a)2^aH *p dz.                                                                                                                   (1.45)

z=0

Согласно закону Ампера 2паНф (z)=Iz (z), что позволяет записать окончательный результат:

Pz=- J Ez (z, p = a)I *z (z)dz.                                                                                                                   (1.46)

Скачать файл