Бинарные деревья. Процедуры, необходимые для работы с бинарными деревьями. Структура хранения бинарных деревьев

Лекция 10. БИНАРНЫЕ ДЕРЕВЬЯ.

Дерево называется m-арным, если полустепень исхода для каждой его вершины не превышает m. При m равном двум имеет место бинарное дерево. Упорядоченные бинарные деревья называют также позиционными бинарными деревьями. Для вершин позиционного бинарного дерева естественно использовать термины «отец», «левое поддерево», «правое поддерево», «левый сын», «правый сын».

Префиксный код бинарного дерева.

Существует естественный способ описания (или идентификации) каждой вершины бинарного дерева с использованием двоичного алфавита. Корень характеризуется пустой строкой, а идентификатор любой другой вершины состоит из префикса, который является кодом отца и окончания, которое для левого сына является нулем, а для правого – единицей.

Префиксным кодом дерева называется множество строк, соответствующих листьям дерева. Это естественный способ отображения структуры бинарного дерева в памяти ЭВМ.

Процедуры, необходимые для работы с бинарными деревьями.

Набор процедур, необходимых для программной реализации структур типа позиционного бинарного дерева, должен обеспечить возможность реализации всех запросов, возникающих в различных приложениях. Практика выявила необходимость включения в такой набор следующих процедур:

Info(p) – возвращает содержимое узла по указателю р;

Left(p), right(p) – возвращают соответственно указатели на левого и правого сына вершины с адресом р;

Father(p) – возвращает указатель на отца заданного узла;

Brother(p) – возвращает указатель на брата заданной вершины;

Isleft(p), isright(p) – возвращает значение «истина», если р указывает на вершину соответственно с левым или правым сыном;

MakeTree(x) – возвращает указатель на корень вновь созданного дерева с информационным полем x в его корне;

Setleft(p,x), setright(p,x) – создают соответственно левого либо правого сына с заданным информационным полем и возвращают указатель на вновь созданную вершину.

Еще одна обычная операция – прохождение бинарного дерева. Очевидный порядок прохождения узлов линейного списка – от первого к последнему, либо наоборот. Для узлов дерева такого естественного порядка не существует. Поэтому прохождение дерева связано с некоторой целостной концепцией, которая обычно использует рекурсивную природу дерева.

Рассмотрим пример использования указанных выше процедур для формирования дерева по префиксному коду. Например, префиксный код  может представлять собой множество:

{ (0,0), (101) }.

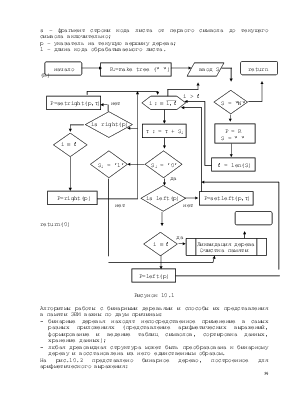
Рассмотрим блок-схему алгоритма формирования бинарного дерева по префиксному коду с использованием перечисленных выше процедур. В блок-схеме используем следующие переменные:

s – идентификатор очередного листа;

s – i-ый символ кода листа.

s – фрагмент строки кода листа от первого символа до текущего символа включительно;

p – указатель на текущую вершину дерева;

l – длина кода обрабатываемого листа.

    начало          R_i=make tree (" ")        ввод S        return (R)

 

                                          i > l

   P=setright(p,t)   нет                     S = "N"

               is right(p)

                               t : = t + S_i            P = R

                                                     S = " "

     

                 S_i = '1'        S_i = '0'            l = len(S)

                                      да

     P=right(p)                is left(p)       P=setleft(p,t)

нет                 нет

return(0)

                                        да

                                         Ликвидация дерева

Очистка памяти

 

                             P=left(p)

Рисунок 10.1

Алгоритмы работы с бинарными деревьями и способы их представления в памяти ЭВМ важны по двум причинам:

-  бинарные деревья находят непосредственное применение в самых разных приложениях (представление арифметических выражений, формирование и ведение таблиц символов, сортировка данных, хранение данных);

-  любая древовидная структура может быть преобразована к бинарному дереву и восстановлена из него единственным образом.

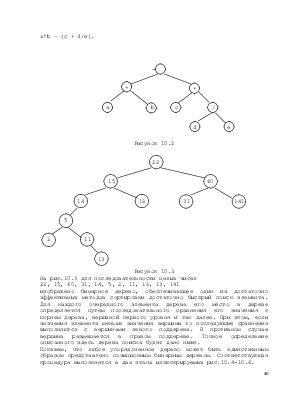
На рис.10.2 представлено бинарное дерево, построенное для арифметического выражения:

а*b – (c + d/e).

-

    *                   +

    a            b      c          /

                                  d         e

Рисунок 10.2

                                 22

 

15                           60

 

14                18           31             141

 

5

 

2          11

 

13

Рисунок 10.3

На рис.10.3 для последовательности целых чисел

22, 15, 60, 31, 14, 5, 2, 11, 18, 13, 141

изображено бинарное дерево, обеспечивающее один из достаточно эффективных методов сортировки достаточно быстрый поиск элемента. Для каждого очередного элемента дерева его место в дереве определяется путем последовательного сравнения его значения с корнем дерева, вершиной первого уровня и так далее. При этом, если значения элемента меньше значения вершины то последующие сравнения выполняются с вершинами левого поддерева. В противном случае вершина размещается в правом поддереве. Точное определение описанного здесь дерева поиска будет дано ниже.

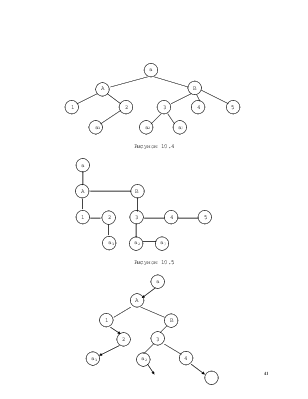
Покажем, что любое упорядоченное дерево может быть единственным образом представлено позиционным бинарным деревом. Соответствующая процедура выполняется в два этапа иллюстрируемых рис.10.4-10.6.

a

 

                  A                          B

 

1               2          3         4         5