This is an oversimplification, but it greatly simplifies the analysis of many string algorithms and data structures. We adopt the assumption for most of this write-up.
A set 5 of strings is prefix free if no string of 5 is a prefix of another. Similarly, 5 is substring free if no string of S is substring of another. A subtring free set is also prefix free.
1.2 Trie
Trie is the basic data structure underlying the suffix tree. A trie is a rooted tree whose edges are labelled with characters so that the labels on the edges from a node to its children are all different (See Figure 1.1). A node of a trie represents the string resulting from the concatenation of the labels on the path from the root to the node. In particular, the root represents the empty string. Because of the uniqueness of child edge labels, no two nodes can represent the same string.
The trie, also known as the digital search tree, is a useful data structure for storing a set of strings. For a set <S of strings, let Trie(<S) denote the unique smallest trie that represents all strings of <S. For simplicity, we assume that S is prefix free. Then, the set of strings represented by the leaves of Trie(*5) is exactly 5. An example is shown in Figure 1.1. If n is the total length of the strings of 5, the space requirement of Trie(<S) is O(n) and it can be constructed in time O(n). Checking whether a string P of length m is in «S, and locating the leaf representing it, if it is, takes O(m) time.
For us, a more interesting problem is the prefix matching problem: Given a (prefix free) set 5 of strings and a pattern P, find the strings of <S that contain P as a prefix. For example, for the string set of Figure 1.1 and pattern pot, the answer is potato and pottery. An algorithm solving this problem using Trie(5) is given below. For a node u and a character c G S, let child(u,c) be the child of u whose edge is labelled with c if it exists and _L otherwise.
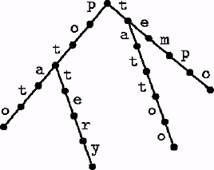
Figure 1.1: Trie(»S) for S = {potato, pottery, tattoo, tempo}.
Prefix matching
i := 0; u := root of Trie(5) % invariant: u represents P[l.. .*] while i < m and child(u, P[i + 1]) ^ _L do
* + +; u :=child(w,P[*]) if i — m then report-subtree('u)
report-subtreefy)
if u is a leaf then report u % u represents a string of S with prefix P else forall children v of u do report-subtreefv)
We did not specify how the operation childfu, c) is implemented. In general, the implementation is not a trivial issue, but under the constant alphabet assumption, any reasonable implementation has a constant time and space complexity. Then, the time requirement of the algorithm is O(m + /en), where len is the total length of the reported strings. We will later see how the time can be reduced to O(m + occ), where occ is the number of the reported strings.
1.3 Aho—Corasick algorithm
Let us consider briefly a generalization of the exact matching problem, the string set matching (multi-pattern matching] problem. Given a set P of patterns and a text T, the task is to find all occurrences of all the patterns in T. For simplicity, we assume that the set of patterns is substring free (and thus prefix free). The problem could be solved separately for each pattern, but there are more efficient algorithms. We describe the main ideas of the Aho-Corasick algorithm, which is the best-known algorithm for this problem.
The Aho-Corasick (AC) algorithm is a generalization of the Morris-Pratt algorithm. The basic idea is to augment the trie Trie('P) with failure links corresponding to the failure function of the MP algorithm. For all nodes u of Trieff) except the root, let F(u) be the node of Trieff) that represents the longest proper suffix of the string represented by u. The trie TrieCP) augmented with the failure links is called the Aho-Corasick (AC) automaton. An example is shown in Figure 1.2. The MP automaton is essentially the AC automaton for a single string.
The AC algorithm is given below. A comparison to the MP algorithm shows clearly their close relation. The algorithm uses Pu to denote the pattern represented by a leaf u.
1.4. SUFFIX TRIE
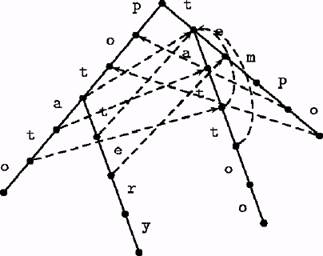
Figure 1.2: The AC automaton for "P = {potato, pottery, tattoo, tempo}. The dashed lines are failure links. For clarity, failure links to the root are not shown.
Aho—Corasick algorithm (for substring free pattern set)
build TrieCP) with failure function F
j := 0; u := root % invariant: u represents T[i .. .j] for some i
while j < n do
while j < n and child(«,T[j + 1]) ^ _L then
j ++• u := ch\\d(u,T\j]} ifu is leaf then
report that T\j — \PU\ 4- 1... j] is an occurrence of Pu if u is root then j + + else u := F(u)
It is not difficult to show that the algorithm runs in O(n) time
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.