Фильтры типов волн и частотно-избирательные фильтры, страница 3

, емкости .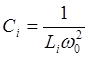

В параллельных контурах – емкости

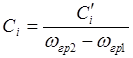, индуктивности .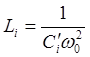

Для того чтобы получить решектороный фильтр из фильтра-прототипа необходимо последовательно использовать оба последних преобразования.

.

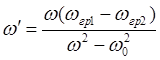Расчет фильтра.

Исходные данные:

-  величена затухания на определенной частоте в полосе затухания ;

-  величина затухания в полосе пропускания ;

-  граничная частота ;

-  сопротивления  и

1. Определяем число звеньев

, для фильтра Баттерворта.

для фильтра Чебышева.

(Последнюю формулу необходимо уточнить)

При вычислениях удобно использовать выражение

.

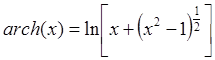Полученное из расчета число звеньев округляется до ближайшего большего числа.

Для фильтра Баттерворта  - параметры определяются по следующим формулам:

.

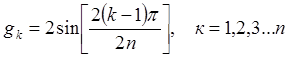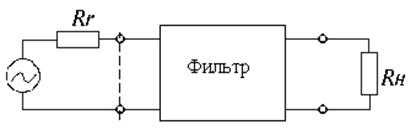
Рис.

Для фильтра Чебышева: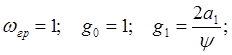

,

,

.

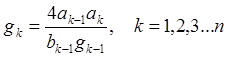
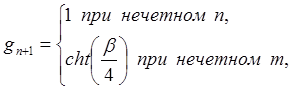
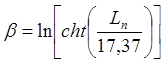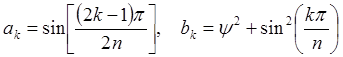При нечетном  величины  распределены симметрично относительно середины фильтра, при четном  симметрия нарушается. В последнем случае можно с помощью фильтра согласовать неравные сопротивления.

Примеры расчета фильтров, а также программа расчета приводится в книге Фуско В. Цепи СВЧ. –М.; Радио и связь, 1990. –228с.

Практические конструкции фильтров.

Фильтры на коаксиальных линиях.

Конструкция фильтра нижних частот имеет вид

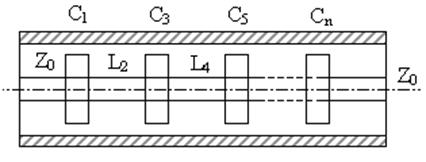
Рис.

Конструкция фильтра верхних частот имеет вид

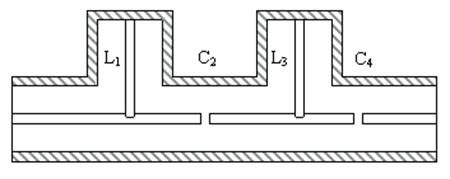
Рис.

Конструкция заграждающего фильтра.

Рис.

В качестве параллельных ветвей используются короткие короткозамкнутые шлейфы с большим волновым сопротивлением, связь которых с основной линией носит емкостный характер. Получаются последовательные контуры. Роль параллельных контуров, включенных в линию последовательно играют четверть волновые отрезки. Схема заграждающего фильтра имеет вид

Рис.

Преобразование фильтров-прототипов в эквивалентные схемы, содержащие инверторы сопротивления или инверторы проводимости и реактивные элементы только одного типа.

Идеальные инверторы сопротивления ведут себя на всех частотах подобно четвертьволновому отрезку линии передачи с волновым сопротивлением . Поэтому, если они нагружены с одной стороны на сопротивление , то сопротивление   со стороны других зажимов будет равно

.

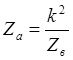Аналогичное представление справедливо и для идеального инвертора проводимости с волновой проводимостью

.

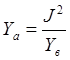На рисунке показаны инверторы сопротивления и проводимости.

Рис.

Из выражений видно, что вследствие преобразования, осуществленного инвертором, последовательная индуктивность с инвертором на каждой стороне будет выглядеть как параллельная емкость, если смотреть со стороны внешних (по отношению к индуктивности) зажимов инвертора.

Аналогично параллельная емкость с инверторами на обеих сторонах окажется последовательной индуктивностью, если смотреть со стороны внешних зажимов инверторов.

Это свойство позволяет преобразовать цепи фильтра-прототипа в любую из эквивалентных форм, показанных на рисунке, которые имеют характеристики передачи точно такие же как у прототипа

Рис.  Фильтр-прототип с инверторами сопротивления.

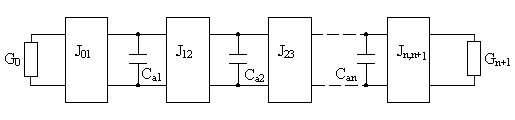
Рис.  Фильтр-прототип с инверторами проводимостей.

Здесь

.

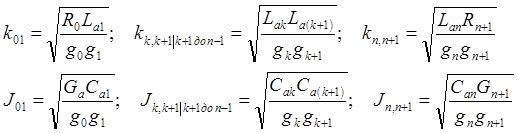Из формул видно, что инверторы обладают способностью изменять уровень сопротивлений или проводимостей в зависимости от выбора значений  или . Поэтому сопротивления  и  могут быть выбраны произвольно и характеристика будет идентична характеристике исходного прототипа, при условии что  определяется по приведенным ранее формулам.

В качестве элементов полосовых и заграждающих фильтров также применяются резонаторы, имеющие как непосредственную связь друг с другом, так и с помощью инверторов. Особенно широко такие фильтры применяются в микрополосковых  устройствах.

Волноводные фильтры.

Фильтр нижних частот на рифленом волноводе.

Волновод имеет поперечные пазы, как показано на рисунке

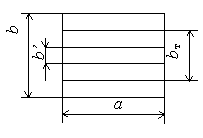
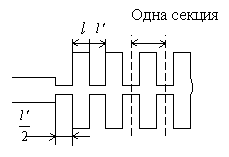
Рис.  Волноводный полосно-пропускающий фильтр.

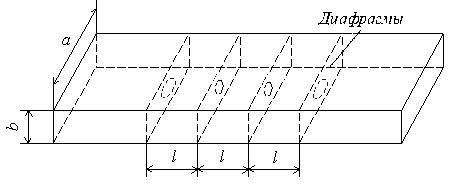
Рис.  Полосно-пропускающий фильтр на резонаторах с непосредственными связями.

Волноводный заграждающий фильтр с четверть волновыми короткозамкнутыми отрезками в качестве параллельного резонансного контура, включенного в волновод последовательно

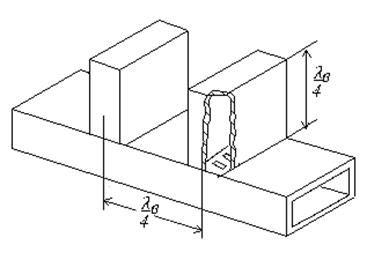
Рис. 2. Резонаторы с четверть волновыми элементами и щелевыми элементами связи.

Эквивалентная схема заграждающего фильтра имеет вид, показанный на рисунке.

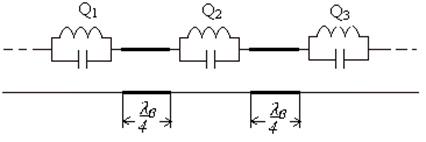
Рис. 2. Эквивалентная схема решекторного фильтра.

Полосковые фильтры.

Фильтр нижних частот.

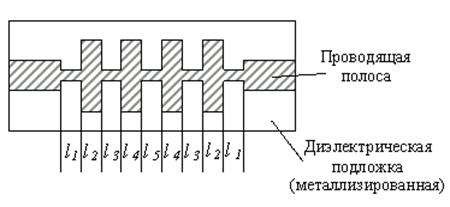
Рис. Топология.

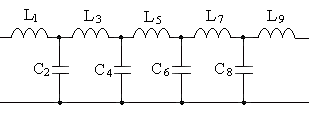
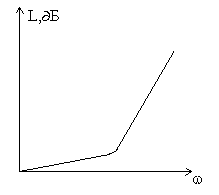
Рис.  Эквивалентная схема.    Частотная характеристика.

Фильтр верхних частот.

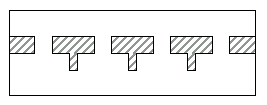
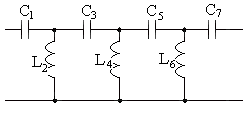
Рис.  Топология.                     Эквивалентная схема.

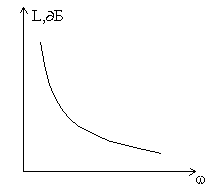
Рис.  Частотная характеристика.

Полосно-пропускающий фильтр.

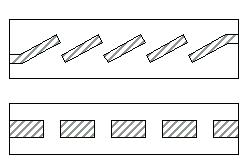
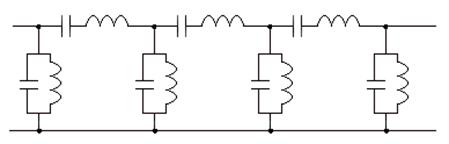
Рис. Топология.                      Эквивалентная схема.

Рис. Частотная характеристика.

Решекторный фильтр.

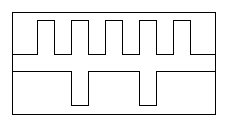
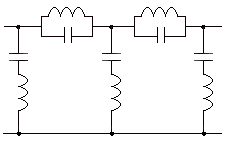
Рис.  Топология.           Эквивалентная схема.

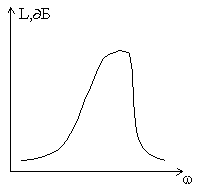
Рис.  Частотная характеристика.