Уравнение неразрывности или сплошности потока. Дифференциальные уравнения движения Эйлера. Практические приложения уравнения Бернулли

ЛЕКЦИЯ 5

Основные уравнения гидравлики

Уравнение неразрывности или сплошности потока.

Дифференциальные уравнения движения Эйлера.

Дифференциальные уравнения движения Навье–Стокса.

Уравнение Бернулли.

Практические приложения уравнения Бернулли.

Для решения практических задач в технической механике жидкости используются более простые зависимости, которые, тем не менее, имеют достаточно общий характер. К числу таких основных уравнений гидравлики относятся:

1) уравнение неразрывности или сплошности потока – уравнение баланса расхода жидкости;

2) дифференциальные уравнения движения жидкости Эйлера;

3) дифференциальные уравнения движения Навье–Стокса;

4) уравнение энергетического баланса потока жидкости – уравнение Бернулли;

3) уравнение баланса количества движения.

5.1. Уравнение неразрывности или сплошности потока

При движении потока жидкости обычно происходят изменения не только скорости частиц, но и ее физических свойств – плотности, вязкости, которые в свою очередь зависят от температуры и давления. При неустановившемся движении физические свойства изменяются не только в пространстве, но и во времени. Например, .

В бесконечно малый параллелепипед (см. рис. 3.1), объем которого dV = dxdydz, за время τ вдоль оси х поступит через грань dydz количество массы жидкости, равное . За то же время из противоположной грани параллелепипеда на расстоянии (x + dx) выйдет количество жидкости, равное .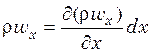

Изменение массы жидкости в объеме параллелепипеда в направлении оси х составит:

.

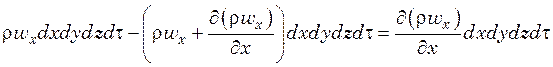Аналогично по направлению осей y и z это изменение составит соответственно

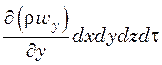   и   .

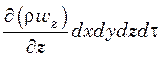Согласно закону сохранения массы за время dτ суммарное изменение массы жидкости по всем трем направлениям в объеме параллелепипеда dv должно быть равно 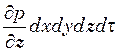. В результате несложных математических преобразований получаем уравнение неразрывности:

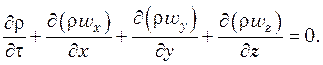                                        (5.1)

Для установившегося потока  и уравнение неразрывности в дифференциальной форме приобретают вид:

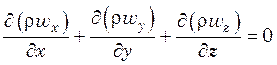                      .                         (5.2)

В потоке несжимаемой жидкости  = const и уравнение упрощается:

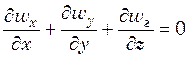                             .                                (5.3)

Для одномерного неустановившегося потока сжимаемой жидкости, направленного вдоль оси х и проходящего через сечение S, уравнение неразрывности можно представить в виде

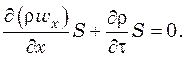                                                               (5.4)

Тогда для установившегося потока

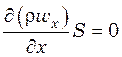  либо

Это значит, что в каждом сечении потока расход жидкости останется постоянным, т.е.:

Из уравнения (5.5) следует, что скорости обратно пропорциональны площадям живых сечений потока.  Для трех различных сечений (1 – 1, 2 – 2 и 3 – 3) трубопровода (на рис. 5.1) имеем

                                          (5.5)

или

где  – массовый расход жидкости, кг/с.

Для капельных жидкостей , и уравнение (5.5) принимает вид .

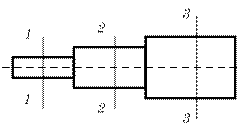
Рисунок 5.1 – К выводу уравнения постоянства расхода.

Выражение (5.5) представляет собой уравнение неразрывности (сплошности) потокав его интегральной форме для установившегося движения.  Уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.

В некоторых случаях, например при вскипании жидкостей вследствие резкого понижения давления, образуется пар, что может привести к разрыву потока. В таких условиях уравнение неразрывности потока не выполняется.

5.2. Дифференциальные уравнения движения Эйлера

Рассмотрим установившийся поток идеальной жидкости, движущейся без трения. Как и при выводе уравнений равновесия Эйлера, выделим в потоке элементарный параллелепипед объемом , ориентированный параллельно осям координат. Ранее было показано, что проекции сил тяжести и давления, действующих