





7. Понятие об устойчивости решений однородных ДУ с систем однородных ДУ.
7.1 Понятие о фазовом пространстве ДУ.
В евклидовом
пространстве с прямоугольными кординатами ![]() решение
решение ![]() системы
системы 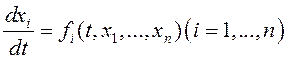 (7.1
)
(7.1
)
определяет закон
движения по некоторой траектории в зависимости от изменения параметра t, который считают
временем, тогда ![]() – скорость точки,
– скорость точки, ![]() -
координаты скорости той же точки.
-
координаты скорости той же точки.
При этой
интерпретации в весьма естественных физических и механических задачах систему 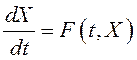 (7.1) называют динамической; пространство с
координатами
(7.1) называют динамической; пространство с
координатами ![]() – фазовым;
а
кривая – фазовой траекторией.
– фазовым;
а
кривая – фазовой траекторией.
Динамическая
система (7.1) определяет в заданный момент времени t в пространстве ![]() поле
скоростей. Если вектор-функция Fзависит от времени,
то фазовые траектории могут пересекаться, если же F не зависит от
времени, то фазовые траектории не перекаются и движение будет стационарным.
поле
скоростей. Если вектор-функция Fзависит от времени,
то фазовые траектории могут пересекаться, если же F не зависит от
времени, то фазовые траектории не перекаются и движение будет стационарным.
Пример: 1. ![]()
Воспользовавшись методом сведения к уравнению второго порядка, найдем решение:
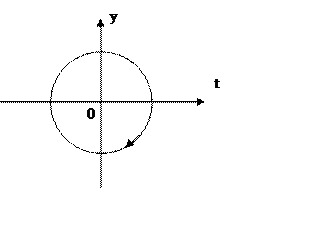
![]() .
.
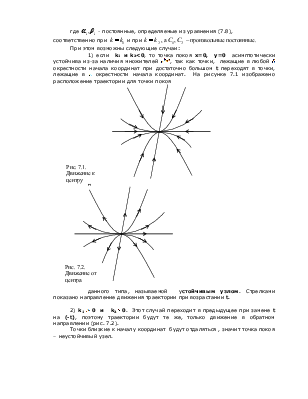
Рассматривая время как параметр, получим семейство окружностей с центром в начале координат.
Правая часть этой
системы удовлетворяет теореме о существовании и единственности решения и не
зависит от времени, следовательно, траектории не пересекаются. Фиксируя ![]() получаем траекторию, причем различным
получаем траекторию, причем различным![]() соответствуют различные начала движения.
соответствуют различные начала движения.
При ![]() фазовые траектории соответствуют точке 0,
которая называется точкой покоя системы.
фазовые траектории соответствуют точке 0,
которая называется точкой покоя системы.
8.2 Устойчивость по Ляпунову
При математическом описании некоторых процессов происходит некоторое огрубление, так как мы не учитываем факторы, незначительно влияющие на процесс. Возможно, что неучтённые факторы сильно влияют на процессы, меняя его количественные и качественные характеристики. Можно указать условия, при котором упрощения невозможны.
Если
некоторые явления описываются системой ДУ: 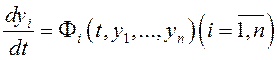 (7.2).
(7.2).
С начальными условиями ![]() , которые обычно
являются результатом измерений и получены с некоторой погрешностью. Возникает
естественный вопрос, можем ли мы пренебречь погрешностью измерений.
, которые обычно
являются результатом измерений и получены с некоторой погрешностью. Возникает
естественный вопрос, можем ли мы пренебречь погрешностью измерений.
Если окажется, что сколь угодно малое изменение начала решений сильно меняет решение, то такое решение не имеет практического применения.
Итак, возникает
задача о нахождении условий, при которых малое изменение начальных данных
приводит к сколь угодно малым изменениям решения. Теория устойчивости
занимается вопросом как ведёт себя система при изменении t от t0 до ![]() . Решение
. Решение ![]() называется устойчивым по Ляпунову, если
для любого
называется устойчивым по Ляпунову, если
для любого ![]() можно подобрать
можно подобрать ![]() такое,
что для всякого решения
такое,
что для всякого решения ![]() той же системы,
начальные значения которого удовлетворяют неравенствам
той же системы,
начальные значения которого удовлетворяют неравенствам ![]() для
всех
для
всех ![]() справедливы неравенства
справедливы неравенства
![]() , (7.3)
, (7.3)
т.е. близкие по
начальным условиям решения остаются близкими при всех ![]() .
.
Замечание. Если система (7.2) удовлетворяет
условию теоремы о непрерывной зависимости решений от начальных данных, то при
определении устойчивости можно писать ![]() т.к. в силу этой теоремы для
т.к. в силу этой теоремы для ![]() решения остаются близкими при достаточно
близких начальных данных . Если при сколь угодно малом
решения остаются близкими при достаточно
близких начальных данных . Если при сколь угодно малом ![]() хотя бы для одного решения
хотя бы для одного решения ![]() неравенства (7.3) не выполняются, то решение
неравенства (7.3) не выполняются, то решение
![]() называется неустойчивым.
Если решение
называется неустойчивым.
Если решение ![]() не только устойчиво,
но и удовлетворяет условию:
не только устойчиво,
но и удовлетворяет условию:
![]() (7.4).
(7.4).
при начальных
данных не сильно отличающихся ![]() , то решение
, то решение ![]() называется асимптотически устойчивым.
называется асимптотически устойчивым.
Заметим, что из одного условия
(7.3) не следует асимптотическая устойчивость решения ![]() .
.
Пример: 2. Исследовать на устойчивость решения ДУ
![]() , удовлетворяющие начальным условиям
, удовлетворяющие начальным условиям ![]() . Решением является функция
. Решением является функция ![]() . Это решение асимптотически устойчиво,
т.к.
. Это решение асимптотически устойчиво,
т.к.
![]() при
при ![]() , если
, если ![]()
и
![]() .
.
Исследование на
устойчивость решения ![]() системы (7.2)
может быть сведено к исследованию на устойчивость тривиального решения – точки
покоя, расположенной в начале координат. Для этого сделаем замену переменных
системы (7.2)
может быть сведено к исследованию на устойчивость тривиального решения – точки
покоя, расположенной в начале координат. Для этого сделаем замену переменных
![]() (7.5)
(7.5)
Тогда система (7.2) принимает вид:
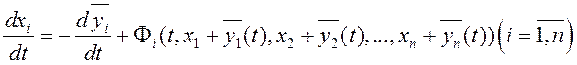 (7.6)
(7.6)
Решению ![]() системы (7.2), которое мы исследуем на
устойчивость, в силу замены
системы (7.2), которое мы исследуем на
устойчивость, в силу замены ![]() соответствует тривиальному решению системы
(7.6), поэтому далее на устойчивость будем изучать точку покоя, расположенную в
начале координат. Это тривиальное решение является точкой покоя. Условия
устойчивости для точки покоя можно сформулировать так: точка покоя
соответствует тривиальному решению системы
(7.6), поэтому далее на устойчивость будем изучать точку покоя, расположенную в
начале координат. Это тривиальное решение является точкой покоя. Условия
устойчивости для точки покоя можно сформулировать так: точка покоя ![]() устойчива в смысле Ляпунова, если для
каждого
устойчива в смысле Ляпунова, если для
каждого ![]() можно подобрать
можно подобрать ![]() такое,
что из неравенства
такое,
что из неравенства 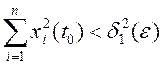
следует
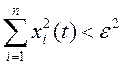
при ![]() .
.
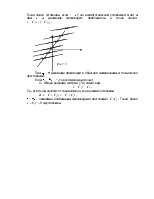
Т. е. траектория начальной точки,
которая находится в ![]() - окрестности начала координат
при
- окрестности начала координат
при ![]() не выходит за пределы
не выходит за пределы ![]() окрестности начала координат.
окрестности начала координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.