Силы Лоренца и Ампера: Учебно-методическое обеспечение практического занятия

3.6. Силы Лоренца и Ампера (2 часа)

3.6.1. Учебная цель занятия

Научить студентов применять следующие понятия и законы: Сила Лоренца. Закон Ампера.

3.6.2. Методические указания к проведению
занятия

Задачи, посвященные действию магнитного поля на проводники с током, включают расчет силы Ампера, действующей со стороны магнитного поля на линейные токи. Рассмотреть различные варианты направления магнитного поля и тока, объяснить правила нахождения направления силы Ампера.

Рассматривая движение заряженных частиц в магнитном поле по окружности, используя второй закон Ньютона определить центростремительное ускорение, радиус окружности и период обращения частицы. Рассмотреть случай, когда скорость частицы образует с направлением однородного магнитного поля угол , отличный от нуля и . В каждом конкретном случае, решение задач сопровождать построением траектории движения частицы. Рассмотреть случай совместного действия электрического и магнитного полей.

3.6.3. Рекомендуемая литература

[3] 5.4, 5.5, 5.9, 5.10; [7] §3.

3.6.4. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

Пример 1. Провод, согнутый в виде трех сторон квадрата, помещен в вертикальное магнитное поле с индукцией  мТл. Конструкция может свободно вращаться вокруг оси , совпадающей с четвертой стороной квадрата. Найти угол отклонения плоскости фигуры от вертикали, если масса единицы длины провода  г/м, а ток в проводе мА. Указать направление тока на рисунке.

Дано:	Решение
мТл = 0,500 Тл;  мА = 0,500 А;  г/м кг/м. ?	Рассмотрим два способа решения. Первый способ. Сначала определим силы Ампера, действующие на три стороны квадрата с током по закону Ампера. Затем определим моменты этих сил.

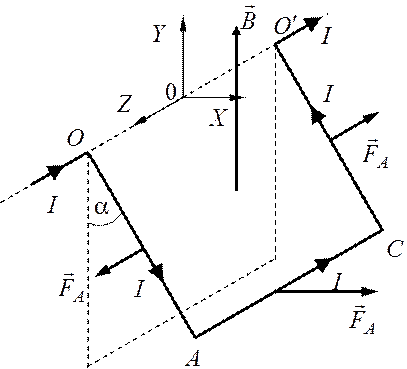На рис. 1.1 показаны силы Ампера, действующие на три провода.

Рис. 1.1

Закон Ампера:

               ,          ,

где  – электрический ток;  – элемент длины провода; вектор  совпадает по направлению с током .

Второй способ. Воспользуемся выражением для вращающего момента, действующего на контур с током в магнитном поле:

              ,            ,              (1.1)

где  – магнитный  момент  контура  с  током,   (здесь  – сила тока;  – площадь контура;  – вектор единичной нормали к контуру, направление которой связано с направлением тока в контуре правилом правого винта).

Рассмотрим подробно второй способ. Чтобы воспользоваться соотношением (1.1), мысленно дополним три проводящие стороны квадрата четвертой проводящей стороной и будем считать, что ток  циркулирует по замкнутому квадратному контуру. Данная процедура не изменит вращательный момент сил магнитного поля относительно оси поворота . Так как сила Ампера, действующая на добавленную сторону квадрата, проходит через ось вращения, то ее момент равен нулю. Выберем направление тока в контуре, как указано на рис. 1.2.

 

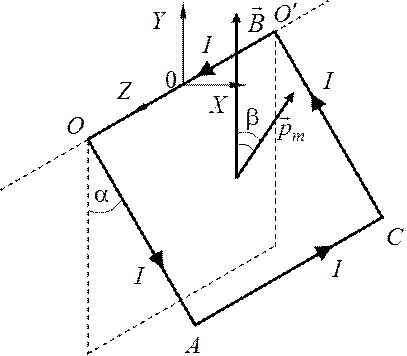Рис. 1.2

Модуль вектора магнитного момента квадратного контура с током

                                        ,

где  – длина стороны квадрата.

Вектор  направлен по нормали к контуру таким образом, что его направление связано с направлением тока правилом правого винта (рис. 1.3).

Вращательный момент, действующий на контур со стороны магнитного поля (1.1),

            ,                    (1.2)

так как  (см. рис. 1.3).

Согласно векторной записи соотношения (1.1), вектор  направлен вдоль оси OZ, т. е. вызывает вращение рамки против часовой стрелки, если смотреть навстречу оси OZ. В положении равновесия вращательный момент магнитного поля скомпенсирован моментом силы тяжести, который вызывает вращение рамки по часовой стрелке и направлен навстречу оси OZ.

 

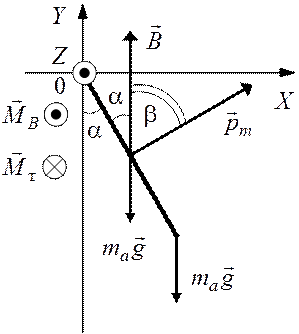Рис. 1.3

Момент силы тяжести

          ,

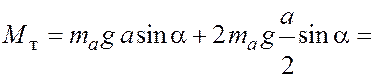
где  – масса стороны квадрата;  – ускорение свободного падения;  – момент силы тяжести, действующей на сторону  (см. рис. 1.2); 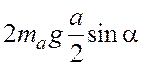 – момент силы тяжести, действующей на стороны  и  (считаем, что сила тяжести боковых сторон приложена в их серединах – центрах масс).

Приравнивая моменты  и  и учитывая, что масса стороны , получаем уравнение

                              ,

позволяющее найти угол ,

                                      .

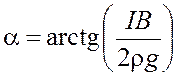Произведем вычисления:

        .

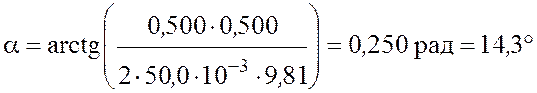Ответ: .

Пример 2. Металлический стержень длиной  мм расположен перпендикулярно бесконечно длинному прямому проводу, по которому течет ток силой  А. По стержню течет ток силой  А. Расстояние от провода до ближайшего конца стержня  мм. Найти силу Ампера, действующую на стержень.

Дано:	Решение
А;  А;  мм м;  мм мм. ?	Взаимное расположение стержня и провода покажем на рис. 2.1. Магнитное поле, создаваемое бесконечно длинным проводом с током, неоднородно: его индукция убывает с удалением от провода, подчиняясь соотношению

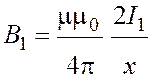                                        .                                        (2.1)

Направление магнитного поля определено по правилу правого винта и показано на рис. 2.1.

 

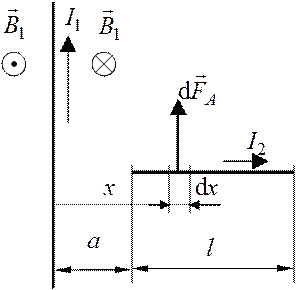Рис. 2.1

На расстоянии  от проводника выделим элемент стержня длиной . Будем считать, что в пределах расстояния  магнитное поле однородное. На элемент стержня длиной  действует сила Ампера  (см. рис. 2.1)

                                  .

Для определения силы, действующей на весь стержень, необходимо провести интегрирование по всей длине стержня. Поскольку направление тока  перпендикулярно магнитному полю , то  по всей длине стержня