МАТЕМАТИЧЕСКИЕ МОДЕЛИ ТЕПЛОВОГО ОГРАЖДЕНИЯ
Математическая модель изоляции основана на представлении теплового ограждения в виде неограниченной многослойной пластины (см. 2.1).
Такое представление оправдано тем, что толщина пластины, которая составляет от 0,05 до 0,20 м, на порядок меньше линейных размеров ИУ. Перенос теплоты через ограждение происходит преимущественно вдоль оси Х.
Математическая модель ограждения должна обеспечить вычисление изменений поля температур и энтальпии по заданным граничным условиям.
Учитывая опыт построения математической модели объекта ОКВ (см. 1.3), а также по соображениям унификации программных продуктов и алгоритмов, для построения математической модели теплового ограждения рационально использовать одномерное уравнение энергии:
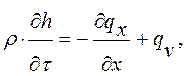 (2.3.30)
(2.3.30)
где, ![]() –
подвод теплоты от внутренних источников, в изоляционной конструкции
–
подвод теплоты от внутренних источников, в изоляционной конструкции ![]() , поэтому форма уравнения энергии предельно
упрощается:
, поэтому форма уравнения энергии предельно
упрощается:
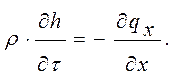 (2.3.31)
(2.3.31)
При замене в уравнении (2.3.31) производных конечно-разностными приближениями получено:
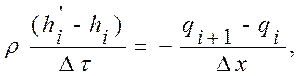 (2.3.32)
(2.3.32)
где ![]() – энтальпия в произвольной ί-ой точке в момент времени τ+∆τ;
– энтальпия в произвольной ί-ой точке в момент времени τ+∆τ;
![]() – соответственно подвод теплоты от узловых
точек; qv – подвод теплоты от внутренних
источников в объеме, отнесенном к ί-ой точке.
– соответственно подвод теплоты от узловых
точек; qv – подвод теплоты от внутренних
источников в объеме, отнесенном к ί-ой точке.
Решая уравнение (2.3.31) относительно ![]() ,
получаем:
,
получаем:
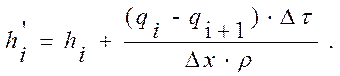 (2.3.32)
(2.3.32)
Перенос теплоты вдоль оси Х определяется законом Фурье:
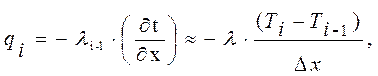 (2.3.33)
(2.3.33)
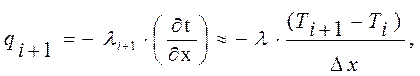 (2.3.34)
(2.3.34)
где Dx – расстояние между точками (шаг разбиения).
От внутренней поверхности моделируемого объекта (при i=1) теплота отводится посредством конвективной теплоотдачи:
![]() , (2.3.35)
, (2.3.35)
где a – коэффициент теплоотдачи; T1 – температура теплоотводящей среды.
К наружной поверхности моделируемого объекта (при i=ni) теплота подводится из окружающей среды посредством конвективной теплоотдачи:
![]() (2.3.36)
(2.3.36)
Выражения (2.3.35) и (2.3.36) определяют граничное условие третьего рода для наружной и внутренней поверхности теплового ограждения.
Для
повышения точности расчетов целесообразно для каждого узла составлять локальный
тепловой баланс. Вычисления изменения величины энтальпии узловых точек
выполняются от поверхности полуограниченного тела. Для поверхности ![]() подвод теплоты от предстоящей точки
определяется интенсивностью конвективного охлаждения (2.3.35).
подвод теплоты от предстоящей точки
определяется интенсивностью конвективного охлаждения (2.3.35).
Подвод теплоты от последующей точки, при i+1=2, рассчитывается по выражению 2.3.37:
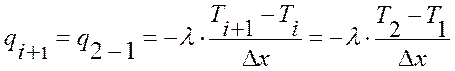 (2.3.37)
(2.3.37)
При переходе к вычислениям для второй точки массива, при i=2, подвод теплоты от предыдущей точки определяется выражением:
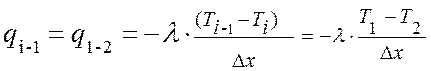 (2.3.38)
(2.3.38)
В тоже время выполнять вычисления этого потока теплоты необязательно,
т.к. он уже вычислялся для точки ![]() . Используя числовые индексы
для тепловых потоков между соседними элементами, можно записать:
. Используя числовые индексы
для тепловых потоков между соседними элементами, можно записать:
![]() (2.3.39)
(2.3.39)
Полученное
аналитическое равенство отражает физический смысл переноса теплоты от одного
узла к другому и является математическим выражением локального теплового
баланса. Используя равенство потоков, можно значительно сократить объем
вычислений, так как для каждого узла (кроме первого) величина ![]() уже была вычислена на предыдущем шаге по
координате. Для учета результатов ранее выполненных вычислений введем буферную
переменную
уже была вычислена на предыдущем шаге по
координате. Для учета результатов ранее выполненных вычислений введем буферную
переменную ![]() , которая используется для описания количества
теплоты, переданного предыдущей точке. Тогда выражение (2.3.32) для всех точек
примет вид:
, которая используется для описания количества
теплоты, переданного предыдущей точке. Тогда выражение (2.3.32) для всех точек
примет вид:
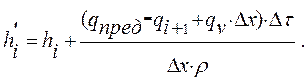 (2.3.40)
(2.3.40)
Для ![]()
![]() . После вычисления величины
. После вычисления величины ![]() производится присвоение
производится присвоение
![]() .
.
Использование буферной переменной не только сокращает объем вычислений, но и сводит к минимуму ошибки вычислений, связанные с использованием приближенных значений, так как неукоснительно соблюдается тепловой баланс узловых точек.
Начальное распределение температур и энтальпий по толщине теплового ограждения зависит от условий конкретного численного эксперимента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.