Обобщением дискретных логик является непрерывная (бесконечнозначная) логика [1,2]. Определяющими операциями в непрерывной логике являются обобщенные дизъюнкция, конъюнкция (аналоговые логические операции амплитудного селектирования) и отрицание:
![]() , (1.34)
, (1.34)
![]() , (1.35)
, (1.35)
![]() ,
(1.36)
,
(1.36)
которые в двухзначной (булевой) логике образуют полную систему функций [3]. Условие (1.36) накладывает требование симметричности множества действительных чисел x относительно его центра (точка 0,5×x0).
Выражения (1.34) и (1.35) являются решением квадратичного уравнения [4]:
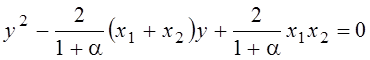 . (1.37)
. (1.37)
Действительно, корни уравнения (1.37) определяются выражением:
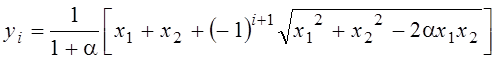 , (1.38)
, (1.38)
где i= 1,2.
Приa = 1 уравнение (1.38) приводится к выражениям (1.34) и (1.35). При этом ![]() и
и ![]() . Таким
образом, определяющие операции (1.34) – (1.36) могут быть выражены через
модуль–функцию
. Таким
образом, определяющие операции (1.34) – (1.36) могут быть выражены через
модуль–функцию ![]() [5] и операцию алгебраического
сложения.
[5] и операцию алгебраического
сложения.
Рассмотрим подкласс линейно–изломных функций, порождаемых классами двухзначных булевых функций одной x и двух x1, x2 переменных (булевый подкласс аналоговых функций), и анализих свойств.
В теоретическом плане это позволяет выделить из всего многообразия линейно–изломных функций подкласс булевых аналоговых функций, т.е. позволяет осуществить идентификацию аналоговых линейно–изломных функций по признаку их соответствия двухзначным булевым функциям.
В практическом плане полученные результаты позволяют осуществлять формальный синтез аналоговых функциональных преобразователей, воспроизводящих подкласс аналоговых булевых функций по известным дискретным схемам путем замены в них двоичных дизъюнкторов и конъюнкторов соответственно на максимизирующие и минимизирующие амплитудные селекторы.
Функциональные преобразователи, воспроизводящие типовые [6] и нетиповые линейно–изломные функции, находят широкое применение в аналоговой вычислительной и информационно–измерительной технике, в системах автоматического управления и регулирования.
Число различных булевых функций, зависящих от n аргументов ![]() конечно
и равно
конечно
и равно ![]() [3].
[3].
При n = 0 в аналоговой области имеем две
независимые от аргумента x
функции ![]() ,
, ![]() и одну линейную функцию
и одну линейную функцию ![]() (рис.1.19).
(рис.1.19).
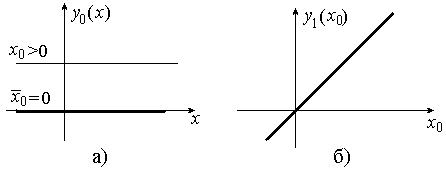
Рис.1.19.
При n = 1 имеем четыре булевых функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В таблице 1.13 приведены числовые значения этих функций при n = 1.
|
x |
y0 |
y1 |
y2 |
y3 |
|
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
В аналоговой области функции y0, y1, y2 и y3 соответственно имеют вид
![]() , (1.39)
, (1.39)
![]() , (1.40)
, (1.40)
![]() ,
(1.41)
,
(1.41)
![]() . (1.42)
. (1.42)
При этом ![]() и
и ![]() , т.е.
функции
, т.е.
функции ![]()
![]() связаны зависимостью
связаны зависимостью
![]() , (1.43)
, (1.43)
где ![]() ,
, ![]() .
.
В дальнейшем изложении аналоговые функции при п = 0,1,2, ... будем называть функциями нулевого, первого, второго и т.д. порядка.
На рис.1.20 представлены графики функций ![]() и
и ![]() при n = 1. Здесь точками изображены числовые значения, соответствующие
при п = 1 булевым функциям, заданным таблицей 1.13. Функции
при n = 1. Здесь точками изображены числовые значения, соответствующие
при п = 1 булевым функциям, заданным таблицей 1.13. Функции ![]() ,
, ![]() ,
, ![]() зависят от константы
зависят от константы ![]() . В частном случае при
. В частном случае при ![]() функции
функции ![]() ,
, ![]() вырождаются в инвертирующую и
неинвертирующую модуль–функции, а
вырождаются в инвертирующую и
неинвертирующую модуль–функции, а ![]() . При
. При ![]() функции
функции ![]() и
и ![]() вырождаются в функции
однополупериодного выпрямления.
вырождаются в функции
однополупериодного выпрямления.
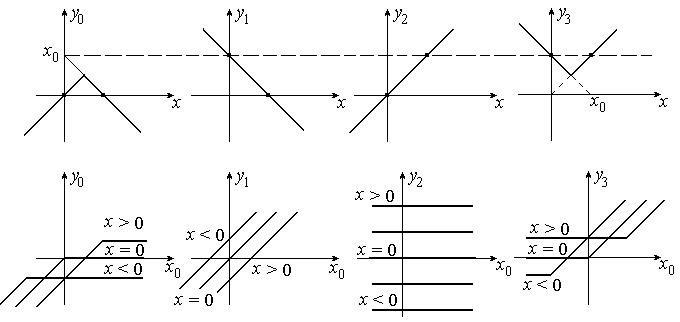
Рис.1.20.
Таким образом, булевы аналоговые функции нулевого порядка не имеют точек
излома. Согласно (1.39) – (1.42), функции первого порядка имеют не более одной
точки излома (функции ![]() и
и ![]() ). При
этом при n = 1 четыре дискретные булевы функции
порождают семь семейств линейно–изломных функций: семейство инвертирующих
модуль–функции
). При
этом при n = 1 четыре дискретные булевы функции
порождают семь семейств линейно–изломных функций: семейство инвертирующих
модуль–функции ![]() со смещением точки излома по
прямой
со смещением точки излома по
прямой ![]() , семейство прямых
, семейство прямых ![]() с отрицательным наклоном и
вертикальным смещением при
с отрицательным наклоном и
вертикальным смещением при ![]() , семейство прямых
, семейство прямых ![]() ,
, ![]() с положительным наклоном и
вертикальным смещением, семейство неинвертирующих модуль–функций
с положительным наклоном и
вертикальным смещением, семейство неинвертирующих модуль–функций ![]() со смещением точки излома по прямой
со смещением точки излома по прямой ![]() , семейство функций формирования
зоны отсечки сверху
, семейство функций формирования
зоны отсечки сверху ![]() и снизу
и снизу ![]() с
регулируемыми уровнями ширины и высоты зоны отсечки и семейство горизонтальных
прямых
с
регулируемыми уровнями ширины и высоты зоны отсечки и семейство горизонтальных
прямых ![]() .
.
Перейдем к рассмотрению аналоговых линейно–изломных функций второго
порядка (n = 2). Здесь порождающим является
класс дискретных булевых функций ![]() двух аргументов
двух аргументов ![]() ,
, ![]() , представленный в табл.1.14.
, представленный в табл.1.14.
Таблица 1.14
|
x1 |
x2 |
z0 |
z1 |
z2 |
z3 |
z4 |
z5 |
z6 |
z7 |
z8 |
z9 |
z10 |
z11 |
z12 |
z13 |
z14 |
z15 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Заданная булева функция в дискретной области может быть представлена в различных эквивалентных формах. Например, для функции Вебба (стрелка Пирса) можем записать
![]() ,
,
![]() .
.
В аналоговой области эти выражения соответственно имеют вид
![]() , (1.44)
, (1.44)
![]()
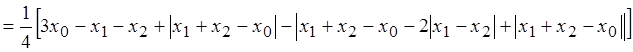 . (1.45)
. (1.45)
Выражения (1.44) и (1.45) определяют различные семейства линейно–изломных функций.
Неоднозначность представления эквивалентных форм булевых функций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.