ЗАДАЧИ ПО ФУНКЦИОНАЛЬНОМУ АНАЛИЗУ
Метрические пространства.
1. Может ли любое подмножество метрического пространства одновременно открыто и замкнуто? Привести пример.
2. Может ли в метрическом пространстве шар большего радиуса содержаться в шаре меньшего радиуса? Привести пример.
3.
В ![]() проверить
аксиомы расстояния для метрики
проверить
аксиомы расстояния для метрики 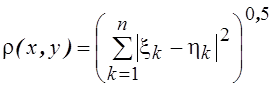 .
.
4.
Сходятся ли в ![]() последовательности
последовательности 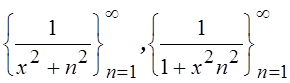 ?
?
5.
Проверить ![]() .
.
6.
Проверить ![]() . Привести контрпример.
. Привести контрпример.
7.
Проверить ![]() .
.
8.
![]() -
метрическое пространство. Проверить, что, если
-
метрическое пространство. Проверить, что, если ![]() -
открытое, то
-
открытое, то ![]() - замкнутое.
- замкнутое.
9.
![]() -
метрическое пространство. Проверить, что, если
-
метрическое пространство. Проверить, что, если ![]() -
замкнутое, то
-
замкнутое, то ![]() - открытое.
- открытое.
10. Множества ![]() открыты. Доказать, что
открыты. Доказать, что 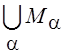 открыто.
открыто.
11.Множества ![]() открыты. Будет ли
множество
открыты. Будет ли
множество 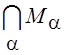 открыто?
открыто?
12.Множества ![]() замкнуты. Доказать, что
замкнуты. Доказать, что
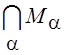 замкнуто.
замкнуто.
13.Множества ![]() замкнуты. Будет ли
множество
замкнуты. Будет ли
множество 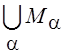 замкнуто?
замкнуто?
14.Пусть ![]() произвольное множество метрического
пространства. Границей множества
произвольное множество метрического
пространства. Границей множества ![]() называется множество
называется множество ![]() таких точек
таких точек ![]() , что
каждый шар с центром в
, что
каждый шар с центром в ![]() содержит хотя бы одну точку из
содержит хотя бы одну точку из ![]() и хотя бы одну точку из дополнения к
и хотя бы одну точку из дополнения к ![]() . Доказать, что
. Доказать, что ![]() замкнутое
множество.
замкнутое
множество.
15.Пусть
![]() непрерывное отображение. Будет ли образ
непрерывное отображение. Будет ли образ ![]() открытого множества
открытого множества ![]() открытым? Если да, обосновать, если нет, привести контрпример.
открытым? Если да, обосновать, если нет, привести контрпример.
16.Пусть
![]() непрерывное отображение. Будет ли образ
непрерывное отображение. Будет ли образ ![]() замкнутого множества
замкнутого множества ![]() замкнут? Если да, обосновать, если нет, привести контрпример.
замкнут? Если да, обосновать, если нет, привести контрпример.
17.Доказать,
что для непрерывности отображения ![]() необходимо и
достаточно, чтобы для любого множества
необходимо и
достаточно, чтобы для любого множества ![]() .
.
18.Доказать,
что для непрерывности отображения ![]() необходимо и
достаточно, чтобы прообраз любого открытого множества
необходимо и
достаточно, чтобы прообраз любого открытого множества ![]() был
открыт.
был
открыт.
19.Точкой
присоединения множества ![]() называется точка, в
любой окрестности которой содержится по крайней мере одна точка множества
называется точка, в
любой окрестности которой содержится по крайней мере одна точка множества ![]() . Является ли точка присоединения
предельной точкой множества? Является ли множество всех точек присоединения данного
множества замкнутым множеством
. Является ли точка присоединения
предельной точкой множества? Является ли множество всех точек присоединения данного
множества замкнутым множеством
20.Привести
пример бесконечного нигде не плотного множества в пространстве ![]() .
.
21.Привести
пример всюду плотного множества в пространстве ![]() .
.
22.Можно
ли ![]() сделать метрическим пространством, если
сделать метрическим пространством, если ![]() . Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
. Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
23.Можно
ли ![]() сделать метрическим пространством, если
сделать метрическим пространством, если 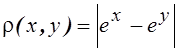 . Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
. Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
24.Можно
ли ![]() сделать метрическим пространством, если
сделать метрическим пространством, если 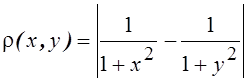 . Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
. Если да, то будет ли оно полным. Если
нет, то, какое пространство является его пополнением?
25.Исследовать
на сходимость в пространстве ![]() последовательность
последовательность 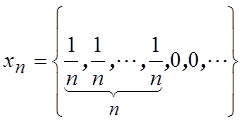 .
.
26.Исследовать
на сходимость в пространстве ![]() последовательность
последовательность 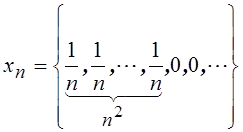 .
.
27.Последовательность
![]() метрического пространства удовлетворяет
условию
метрического пространства удовлетворяет
условию 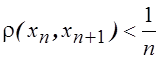 . Будет ли эта последовательность фундаментальна?
Будет ли она компактна?
. Будет ли эта последовательность фундаментальна?
Будет ли она компактна?
28.Доказать компактность множества 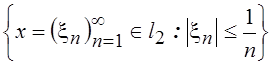 .
.
29.Доказать в ![]() компактность множества
функций вида
компактность множества
функций вида 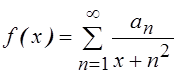 , где
, где ![]() -
произвольная последовательность, для которой
-
произвольная последовательность, для которой ![]()
30.Доказать,
что множество функций ![]() является компактным.
является компактным.
31.Будет ли компактным множество функций из ![]() , котороые имеют ограниченные в
совокупности
, котороые имеют ограниченные в
совокупности ![]() -ые производные?
-ые производные?
32.Доказать, что множество последовательностей с конечным
числом отличных от нуля элементов плотно в ![]() .
.
33.Доказать сепарабельность пространства ![]() непрерывных функций, для которых
непрерывных функций, для которых 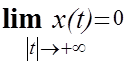 ,
, 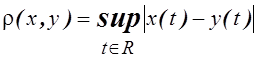 .
.
34.Доказать сепарабельность пространства ![]() последовательностей, стремящихся к нулю.
последовательностей, стремящихся к нулю.
35.Пусть ![]() - дифференцируемая на
отрезке
- дифференцируемая на
отрезке ![]() функция, причем
функция, причем ![]() .
Будет ли уравнение
.
Будет ли уравнение ![]() иметь решение?
иметь решение?
36.Начиная
с какого приближения ![]() точность приближения решения
уравнения
точность приближения решения
уравнения ![]() не превосходит 0,01.
не превосходит 0,01.
37.Используя
принцип сжимающих отображений, найти в ![]() решение уравнения
решение уравнения 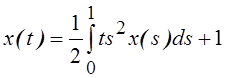 .
.
38.Используя
принцип сжимающих отображений, найти в ![]() решение уравнения
решение уравнения 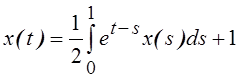 .
.
Нормированные пространства.
1.
Проверить аксиомы нормы
в пространстве 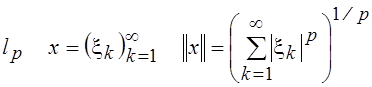 .
.
2.
Проверить аксиомы нормы
в пространстве ![]()
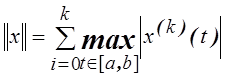 .
.
3.
Является ли нормой в ![]() функция
функция 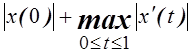 ?
?
4.
Является ли нормой в ![]() функция
функция 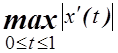 ?
?
5.
Является ли нормой в ![]() функция
функция 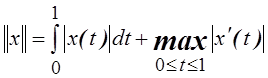 ?
?
6.
Доказать, что замыкание
подпространства ![]() в пространстве
в пространстве ![]() есть пространство
есть пространство ![]() последовательностей,
сходящихся к нулю.
последовательностей,
сходящихся к нулю.
7.
Пусть 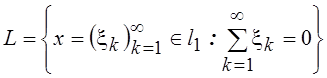 . Образует ли
. Образует ли ![]() подпространство
в
подпространство
в ![]() .
.
8. Доказать эквивалентность норм
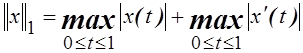 ,
, 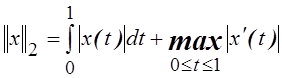
в пространстве ![]() .
.
9.
Доказать, что множество
непрерывных кусочно линейных функций всюду плотно в пространстве ![]() .
.
10.Доказать что всякое конечномерное линейное многообразие в нормированном пространстве есть подпространство.
11.Образуют ли подпространство в ![]() множество
функций, удовлетворяющих условию
множество
функций, удовлетворяющих условию 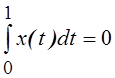 ?
?
12.Образуют ли подпространство в ![]() множество
непрерывно дифференцируемых функций?
множество
непрерывно дифференцируемых функций?
13.Доказать, что ![]() подпространство
в
подпространство
в ![]() .
.
14.Пусть ![]() - всюду плотные
множества. Возможно ли, что
- всюду плотные
множества. Возможно ли, что ![]() ø?
ø?
15.Доказать, что дополнение к нигде не плотному множеству всюду плотно. Справедливо ли обратное утверждение?
16.Пусть ![]() непрерывное
отображениепространства
непрерывное
отображениепространства ![]() на пространство
на пространство ![]() ,
, ![]() - всюду
плотное множество в
- всюду
плотное множество в ![]() . Доказать, что
. Доказать, что ![]() - всюду плотное в
- всюду плотное в ![]() .
.
17.Пусть ![]() , ряд
, ряд 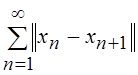 сходится. Доказать,что последовательность
сходится. Доказать,что последовательность ![]() фундаментальна. Верно ли обратное
утверждение?
фундаментальна. Верно ли обратное
утверждение?
Гильбертовы пространства.
1.
Пусть ![]() -
биортогональные системы элементов гильбертова пространства, т.е.
-
биортогональные системы элементов гильбертова пространства, т.е. ![]() . Доказать, что каждая из этих систем
линейно независима.
. Доказать, что каждая из этих систем
линейно независима.
2.
Пусть ![]() и
и 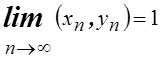 . Доказать, что
. Доказать, что 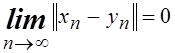 .
.
3.
Доказать, что в гильбертовом
пространстве ![]() из
из ![]() следует,
что
следует,
что ![]() .
.
4.
Рассмотрим линейное пространство непрерывных
на ![]() функций
функций ![]() таких,
что
таких,
что 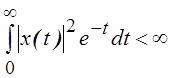 . Проверить, что числовая функция
. Проверить, что числовая функция 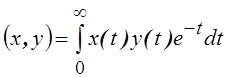 удовлетворяет аксиомам скалярного
произведения. Найти три первых ортонормированных многочлена, полученных путем ортогонализации
системы
удовлетворяет аксиомам скалярного
произведения. Найти три первых ортонормированных многочлена, полученных путем ортогонализации
системы 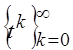 .
.
5.
Пусть 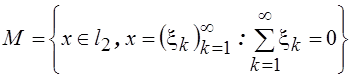 .
Доказать, что
.
Доказать, что![]() - линейное многообразие, всюду плотное в
- линейное многообразие, всюду плотное в ![]() .
.
6.
В пространстве ![]() задана последовательность
задана последовательность 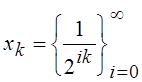 . Доказать, что линейная оболочка этой
последовательности всюду плотна в
. Доказать, что линейная оболочка этой
последовательности всюду плотна в ![]() .
.
Теория операторов.
1.
Будет ли ограничен оператор 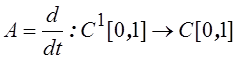 ?
?
2.
Будет ли ограничен оператор 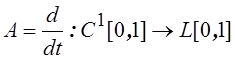 ?
?
3.
Доказать ограниченность
оператора и найти его норму: 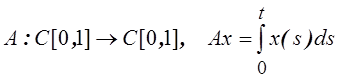 .
.
4.
Доказать ограниченность
оператора и найти его норму: ![]() .
.
5.
Доказать ограниченность
оператора и найти его норму: 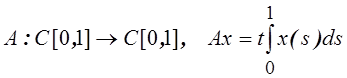 .
.
6.
Доказать ограниченность
оператора и найти его норму: ![]() .
.
7.
Доказать ограниченность
оператора: 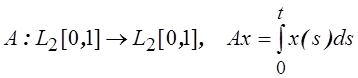 .
.
8.
Оператор ![]() . При каком условии на
. При каком условии на ![]() оператор
оператор ![]() будет
ограниченным и какова при этом его норма?
будет
ограниченным и какова при этом его норма?
Теория Хана-Банаха. Сопряженные пространства.
1.
Доказать, что функционал 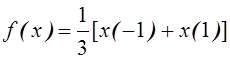 является ограниченным в пространстве
является ограниченным в пространстве ![]() . Найти его норму.
. Найти его норму.
2.
Доказать, что функционал 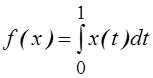 является ограниченным в пространстве
является ограниченным в пространстве ![]() . Найти его норму.
. Найти его норму.
3.
Ограничен ли функционал 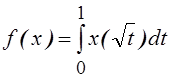 в пространстве
в пространстве ![]() ?
?
4.
Ограничен ли функционал 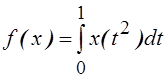 в пространстве
в пространстве ![]() ?
?
5.
Доказать, что функционал 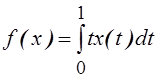 является ограниченным в пространстве
является ограниченным в пространстве ![]() . Найти его норму.
. Найти его норму.
6.
Доказать, что функционал 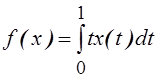 является ограниченным в пространстве
является ограниченным в пространстве ![]() . Найти его норму.
. Найти его норму.
7.
В пространстве ![]() с элементами
с элементами ![]() на подпространстве
на подпространстве
![]() задан линейный функционал
задан линейный функционал ![]() . Найти единственное продолжение
. Найти единственное продолжение ![]() на
на ![]() с
сохранением нормы.
с
сохранением нормы.
8.
Пусть ![]() -
гильбертово пространство,
-
гильбертово пространство, ![]() - подпространство,
- подпространство, ![]() - щграниченный линейный функционал,
заданный на
- щграниченный линейный функционал,
заданный на ![]() . Доказать, что существует единственное
продолжение
. Доказать, что существует единственное
продолжение ![]() на все
на все ![]() с сохранением
нормы.
с сохранением
нормы.
9.
Доказать, что ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.