Свойства детерминантов. Операции сложения и умножения матриц

Определение. Матрицей размеров  называется совокупность  чисел, расположенных в виде таблицы из  строк и  столбцов:

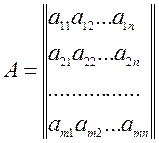
Определение. Детерминант квадратной матрицы – это число, которое ставится в соответствие матрице и может быть вычислено по ее элементам по формуле.

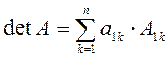
 - элементы  матрицы

- алгебраическое дополнение соответствующего элемента матрицы, которое вычисляется по формуле

где - минор соответствующего элемента матрицы.   

Определение. Минор это детерминант матрицы порядка , полученной из  вычеркиванием  строки и -го столбца.

Определение. Матрица порядка 1 состоит из одного числа, и ее детерминант по определению считают равным этому числу.

Определение. Если в матрице  поменять местами строки и столбцы, то полученная матрица будет называться транспонированной, а переход от к  - транспонирование.

Матрицу, полученную из матрицы  транспонированием, обозначают .

Сформулируем одну очень важную теорему в теории определителей.

Теорема. Для каждой квадратной матрицы порядка  имеет место формула

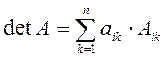
или                                         

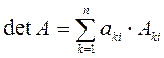
Эти формулы называются формулами разложения детерминанта соответственно по строке и по столбцу.

Свойства детерминантов.

Свойство 1. Для любой квадратной матрицы

Свойство 2. Если элементы одной строки или столбца детерминанта равны нулю, то и детерминант равен нулю.

Свойство 3. Для того чтобы умножить детерминант на число, достаточно умножить на это число строку (столбец).

Свойство 4. Если одна из строк (столбцов) является суммой двух строк (столбцов), то её детерминант есть сумма детерминантов соответствующих матриц.

Свойство 5. Если в матрице поменять местами какие-нибудь две строки (столбца), то ее детерминант изменит знак.

Свойство 6.  Если в матрице есть два две одинаковые строки (одинаковых столбца), то .

Свойство 7. Справедливы следующие формулы

,      

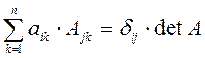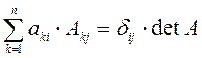
Здесь  - символ Кронекера, который определён следующим образом

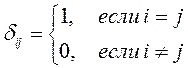
Свойство 8. Детерминант матрицы не изменится, если к какой-нибудь строке (какому  нибудь  ее столбцу) прибавить линейную комбинацию остальных строк (столбцов) этой матрицы.

Определение. Совокупность  чисел  называется решением системы, если каждое уравне­ние системы обращается в тождество после подстановки в него чисел  вместо соответствующих неизвестных .

Теорема (правило  Крамера). Система из  уравнений с  неизвестными

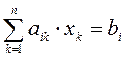
в случае, когда детерминант матрицы системы отличен от нуля, имеет решение и притом только одно. Это ре­шение находится по формулам

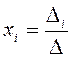
где через  обозначен детерминант матрицы системы, а через  — детерминант матрицы, получаемой из матрицы системы заменой -го столбца столбцом свободных чле­нов.

Лекция 2

Действия с матрицами

Определим операции сложения и умножения матриц. Эти операции широко применяются в различ­ных областях математики.

1.  Сложение и умножение на число.

Определение. Две матрицы мы будем называть равными, если они имеют одина­ковые размеры, и равны их элементы, стоящие на оди­наковых местах.

Пусть  и -  матрицы, состоящие из  строк и  столбцов. Сопоставим им третью матрицу тех же размеров , элементы которой равны сум­мам стоящих на тех же местах элементов матриц  и . Иными словами, элементы матрицы связаны с элементами  и матриц  и равенством

     для всех и .

Определение. Матрица , элементы которой равны

     для всех и .

называется  суммой ма­триц   и  и обозна­чается

Подчеркнем, что сумма определена только для  матриц одних и тех же размеров.

Определение. Матрица , элементы которой равны произведениям      для всех и .

называется произведением  на  и обозна­чается

Из свойств сложения и умножения чисел легко вы­текает следующее утверждение.

Утверждение. Для любых матриц  и и  одних и тех же размеров и любых чисел  и  выпол­нены равенства

1.   - коммутативность сложения.

2.   - ассоциативность сложения.

3.   - дистрибутивность относительно сложения.

4.   - дистрибутивность относительно сложения чисел.

5.  - ассоциативность относительно умножения чисел.

Доказательство этого утверждения вытекает из свойств  действительных чисел.

Матрица, все элементы которой равны нулю, назы­вается нулевой матрицей. Если -  нулевая матрица размеров , то для любой матрицы  тех же раз­меров имеем

Матрицу  мы будем называть противополож­ной матрице иобозначать . Она обладает тем свойством, что

2. Умножение матриц.