Свойства детерминантов. Операции сложения и умножения матриц, страница 3

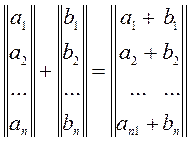
Аналогично суммой двух строк одной и той же длины называется строка, элементы которой равны суммам соответствующих элементов данных строк.

Определение. Произведением столбца на число называется столбец, каждый элемент которого равен соответствующему элементу данного столбца, умножен­ному на это число, т. е. по определению

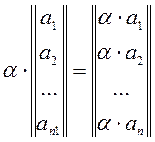
Аналогично умножение строки на число определяется как умножение на это число каждого ее элемента.

Следующее утверждения легко следует из свойств сложения и умножения чисел.

Утверждение. Для любых столбцов р, я и г одинаковой высоты и любых чисел а и р выполнены следующие равенства:

6.   - коммутативность сложения .

7.   - ассоциативность сложения.

8.   - дистрибутивность относительно сложения столбцов.

9.   - дистрибутивность относительно сложения чисел.

Сложение строк и умножение строки на число обла­дают теми же свойствами. Отдельно формулировать мы их не будем.

Определение. Столбец  мы назовем линейной комбинацией столбцов  одинаковой высоты, если он определяется как

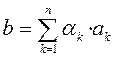
Аналогично определяется линейная комбинация строк.

Определим понятия линейно зависимой и линейно независимой системы столбцов (и те же понятия для строк)

Определение. Система из  столбцов , одной и той же высоты называется линейно независимой, если из равенства

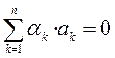
Следует, что . В противном случае, т. е. если существуют  числа , одновременно не равных нулю и таких, что выполнено равенство наше равенство, то си­стема называется линейно зависимой.

Определения линейно зависимой и линейно незави­симой системы строк формулируются дословно так же.

Линейную комбинацию, все коэффициенты которой равны нулю, принято называть тривиальной. С помощью этого термина определение можно сформулировать так. Система столбцов линейно зависима, если существует равная нулю нетривиальная линейная комбинация этих столбцов. Система столбцов линейно независима, если только тривиальная линейная комбинация этих столбцов равна нулю.

Определение. В матрице размером минор порядка г называется базисным, если он отли­чен от нуля, а все миноры порядка  равны нулю, или миноров порядка.

Ясно, что в матрице может быть несколько разных базисных миноров. Все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка  равны нулю, то равны нулю и все миноры порядка , а следовательно, и всех больших поряд­ков. Это становится очевидным, если применить опре­деление детерминанта к какому-нибудь минору порядка : все дополнительные миноры элементов его пер­вой строки являются минорами порядка   нашей матрицы и, следовательно, равны нулю.

Рассмотрим миноры порядка 1, т. е. элементы мат­рицы. Если они все равны нулю, то базисного минора вообще нет. Пусть есть не равный нулю минор по­рядка 1. Найдем все миноры порядка 2. Если все они равны нулю, то любой отличный от нуля элемент мат­рицы является ее базисным минором. В случае, когда существуют отличные от нуля миноры порядка 2, сле­дует рассмотреть миноры порядка 3. Если они все равны нулю, то любой ненулевой минор порядка 2 базисный. Продолжая этот процесс, мы обязательно найдем базисный минор. Может случиться, что суще­ствуют отличные от нуля миноры самого большого возможного порядка. В этом случае любой из них считается базисным.

Определение. Рангом матрицы называется по­рядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если каждый элемент матрицы равен нулю, то ранг такой матрицы по определению считают нулем.

Ранг матрицы мы будем обозначать .

Рассмотрим систему линейных алгебраических уравнений. 

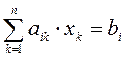
Припишем  к  матрице системы справа столбец сво­бодных членов. Полученную матрицу

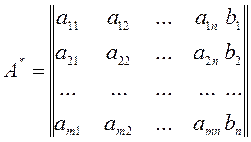
назовем расширенной матрицей.

Сформулируем теорему Кронекера -  Капели

Теорема. Система линейных алгебраических уравнений имеет ре­шение, если ранг матрицы системы равен рангу расширенной матрицы.

Для доказательства перепишем систему, поль­зуясь определением операций со столбцами. Мы по­лучим

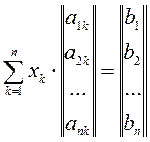
1°. Если существует решение, то столбец свободных членов есть линейная ком­бинация столбцов матрицы системы. Значит, добавление этого столбца не увеличивает общего числа линейно независимых столбцов, и .

2°. Пусть . В этом случае базисный ми­нор матрицы  является базисным и в матрице . Это означает, что столбец свободных членов есть ли­нейная комбинация тех столбцов матрицы , в которых расположен базисный минор, следовательно, столбец свободных членов есть линейная комбинация всех столбцов матрицы . Коэффициенты этой линейной комбинации представляют собой решение системы.