Чтобы восстановить последнее значение, необходимо к последнему сглаженному значению прибавить средний абсолютный прирост.
Пример:
33. Выявление тренда с помощью теоретической прямой
Суть метода наименьших квадратов в следующем: искомые значения должны быть такие, при которых обеспечивалось бы минимальная сумма квадратов их отклонений от фактических значений.
![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
Системы нормальных уравнений и соответственно расчет параметров а0 и а1 упрощаются, если отсчет времени ведется от середины ряда. При нечетном числе уровней серединная точка (год, месяц) принимается за 0, тогда предшествующие периоды обозначаются, соответственно -1;-2 ..., а следующие за средним (центральным) 1, 2 ... При четном числе уровней два серединных момента обозначают -1 и +1, а все последующие и предыдущие, соответственно, через 2 интервала: +-3;+-5;+-7 ...
![]() ,
, ![]() .
.
34. Расчет среднего уровня ряда динамики
В
качестве обобщенной характеристики уровней ряда динамики служит средний уровень
ряда динамики ![]() . В зависимости от типа ряда динамики
используются различные расчетные формулы. Моментные ряды динамики делятся на
равные и неравные. Для равных используется средняя хронологическая простая:
. В зависимости от типа ряда динамики
используются различные расчетные формулы. Моментные ряды динамики делятся на
равные и неравные. Для равных используется средняя хронологическая простая:
![]() . Для неравных –
средняя хронологическая взвешенная:
. Для неравных –
средняя хронологическая взвешенная: ![]() , где
, где ![]() - уровни ряда, сохраняющиеся без
изменения на протяжении интервала времени
- уровни ряда, сохраняющиеся без
изменения на протяжении интервала времени ![]() .
.
Интервальные ряды также делятся на равные и неравные.
Для равных используется средняя арифметическая простая: ![]() . А для неравных средняя арифметическая взвешенная:
. А для неравных средняя арифметическая взвешенная: ![]() , где t –
кол-во периодов, в течении которых предполагается, что значение уровней не
изменяется.
, где t –
кол-во периодов, в течении которых предполагается, что значение уровней не
изменяется.
35. Выявление тренда с помощью полинома второй степени
Если в основе ряда динамики тенденция выражена криволинейной зависимой, то для сглаживания динамического ряда рекомендуется использовать полиномы не высоуих порядков (не выше 3), который позволяет учесть изгибы линии тренда.
![]()
38. Расчет точечного прогноза с помощью уравнения теоретической кривой
Чтобы определить прогнозное значение с помощью теоретической кривой необходимо подставить в уравнение значение уровня, при этом необходимо учесть начала координат и точку отсчета.
Пример:
40. Расчет точечного прогноза на основе среднего абсолютного прироста и среднего темпа роста
Для построения прогнозного значения с помощью среднего абсолютного прироста необходимо к последнему фактическому значению прибавить средние абсолютные приросты столько раз, коков период упреждения.
Если цепные темпы роста фактического ряда динамики примерно одинаковы, то можно предположить, что в основе ряда динамики лежит степенная функция. Поэтому для определения прогнозного значения последнее фактическое значение ряда динамики столько раз умножается на средний темп роста, каков период упреждения.
Пример:
41. Расчет интервального значения прогноза
В анализируемом периоде не совпадают с теоретическим их значения в следствии: субъективного прогноза вызванного теорет.; погрешности расчета параметра уравнения; влияния случайных компонентов. Погрешность связанная со 2-ой и 3-ей величиной может быть учтена доверительным интервалом. Интервальный прогноз определяется и корректируется на величину.
45. Средние из индивидуальных индексов
Включают общий индекс, среднеарифметический индекс физического объема, среднегармонический индекс цен.
![]() ,
, ![]() ,
,![]() Значит:
Значит:![]() .
.
Средний арифметический индекс используется в том случае, если известно значение выручки и изменение объема по каждому виду продукции.
![]() ,
, ![]() ,
, 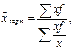 ,
Значит:
,
Значит: ![]() .
.
![]() .
.
46. Агрегатные индексы
Характеризуют относительное изменение показателя в целом по сложной совокупности, отдельные элементы которой несоизмеримы в физических величинах. Вычисляются по товарным группам или нескольким видам продукции.
Агрегатная форма – это исходная основная форма выражения сводного индекса.
1.
Сводный (агрегатный) индекс товарооборота: ![]() .
.
Правило постоянного индекса: кол-во меняется при старом качестве, а качество при старом количестве.
2.
Сводный (агрегатный) индекс цен: ![]() - индекс Пааше.
- индекс Пааше. ![]() - индекс Ласпейреса.
- индекс Ласпейреса.
3.
Сводный (агрегатный индекс) физического объема: ![]() .
.
![]() ,
, ![]() -
перерасход или экономия.
-
перерасход или экономия.
47. Расчет дополнительных характеристик рядов динамики
Абсолютный прирост характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между данным уровнем и предыдущим или начальным. Уровень, который сравнивается, называется текущим, а уровень с которым производится сравнение, называется базисным. Если каждый уровень ряда сравнивается с предыдущим, то получаются цепные показатели. Если же все уровни ряда сравниваются с одним и тем же, первоначальным уровнем, то полученные показатели называются базисными.
Абсолютный прирост определяется по формулам;
цепной: ![]() ; базисный:
; базисный: ![]() ,где
,где ![]() -
текущий уровень ряда;
-
текущий уровень ряда; ![]() - уровень
предшествующий;
- уровень
предшествующий;![]() - начальный
уровень ряда.
- начальный
уровень ряда.
Темпом роста называется отношение данного уровня к предыдущему или начальному, выраженному в процентах.
цепной: ![]() ; базисный:
; базисный: ![]() ;
;
Темпом прироста называется отношение абсолютного прироста к предыдущему или начальному членам ряда, выраженным в процентах;
Темп прироста может быть рассчитан как:
![]()
![]() ;
;
Для характеристики темпов роста и прироста в среднем за весь период вычисляют средний темп роста и прироста.
Средний
абсолютный прирост: ![]() .
.
Средний темп роста рассчитывается по средней геометрической:
![]() ,
,![]()
Абсолютное значение одного процента прироста и
определяется по формуле: ![]()
49. Виды и формы взаимосвязи
Различают два вида взаимосвязей между признаками: функциональную и вероятностную (стохастическую). Функциональная связь – это жесткая, детерминическая (определенная), зависимая, когда каждому значению факторного признака (независимого) соответствует строго определенное значение зависимого (результативного) признака. Пример: выручка = цена * объем. Стохастическая связь - это необратимая, нежесткая зависимость, когда каждому значению факторного признака соответствует целый ряд значений результативного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.