Физика.Краткие сведения из теории. Часть 1, страница 2

Осевые моменты инерции

     

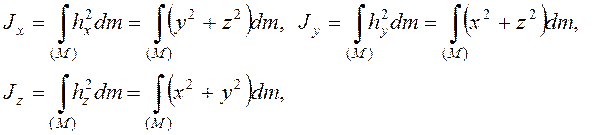
центробежные моменты инерции

      .

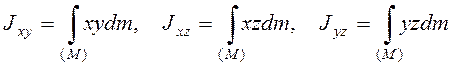Формула, идентичная (1.7), выполняется в связанной с твердым телом системе координат . Здесь матрица моментов инерции при движении твердого тела  остается постоянной. Если связанные оси являются главными осями инерции тела, то , и кинетический момент  .

В частном случае при вращении тела около неподвижной оси  , а составляющая кинетического момента вдоль оси вращения .

Кинетический момент системы относительно неподвижной точки О и произвольной точки Р связаны соотношением

                .                                                                               (1.8)

В частном случае, когда точка Р является центром масс системы С, формула (1.8) принимает вид

                .

Теорема об изменении кинетического момента системы относительно неподвижного полюса О имеет вид

                .

В правой части 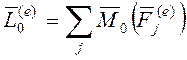 - сумма моментов внешних сил, приложенных к системе, относительно точки О.

Относительно произвольной точки Р формулировка теоремы следующая:

                ,

а в случае, если точка Р совпадает с центром масс системы:

                    .

Если , то . Все вышеприведенные формулы можно записать в проекциях на оси координат .

Так как в правой части теоремы присутствуют моменты внешних сил, характеризующие способность сил к вращению, то теорема об изменении кинетического момента часто применяется при вращательном движении, хотя может быть применена не только в этом случае.

4.  Теорема об изменении кинетической энергии.

Кинетическая энергия материальной точки 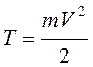. Для твердого тела   .

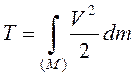С движением центра масс кинетическая энергия системы точек или твердого тела связана соотношением

      ,

где  - скорость точек относительно системы координат, поступательно движущейся вместе с центром масс.

При поступательном движении тела 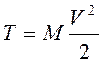 ( - скорость любой точки тела), при вращении тела около неподвижной оси () 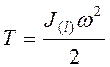, где  - момент инерции тела относительно оси вращения. При плоскопараллельном движении 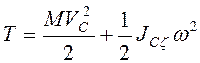, где  - момент инерции тела относительно оси, проходящей через центр масс тела перпендикулярно плоскости движения его точек; или 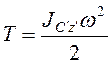, где  - момент инерции тела относительно оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения точек тела.

При вращении тела около неподвижной точки О 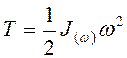, где  - момент инерции тела относительно оси, проходящей через точку О вдоль вектора угловой скорости; или

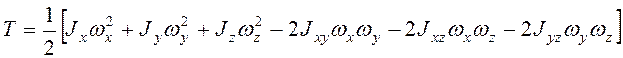     (1.9)

Идентичная формула имеет место при использовании связанной системы координат . Для главных осей инерции тела

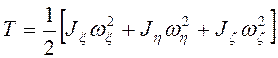.                                                    (1.10)

В общем случае движения твердого тела 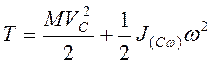, где  –момент инерции тела относительно оси, проходящей через его центр масс вдоль вектора угловой скорости; или 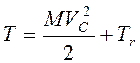, где  вычисляется по формулам, аналогичным (1.9) и (1.10), в системе координат с началом в центре масс тела.

По теореме об изменении кинетической энергии системы в дифференциальной форме

.

В правой части теоремы присутствует элементарная работа приложенных к системе сил

                   

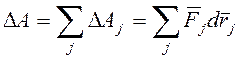
( - радиус-вектор точки приложения силы ). Элементарная работа каждой силы может быть выражена через декартовы и траекторные координаты точки приложения силы:

                   

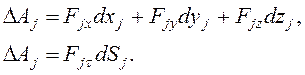
Элементарная работа момента силы, действующей на твердое тело, вращающееся вокруг оси (), определяется формулой

                   

( - угол поворота тела).

Теорема об изменении кинетической энергии системы в конечной форме имеет вид

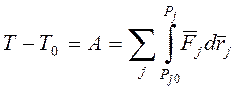                    .                                                          (1.11)

В правой части работа силы представлена в виде криволинейного интеграла второго рода, взятого по пути, проходимому точкой приложения силы, из начального положения  в конечное положение .

Если сила консервативна и стационарна, то ее вектор представим в виде . Функция  называется силовой функцией, соответствующей силе , а  - потенциальная энергия, соответствующая силе . Тогда элементарная работа действующих консервативных сил

                    ,

где .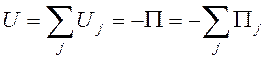

Если работу совершают только консервативные стационарные силы, то (1.11) переходит в  - закон сохранения полной механической энергии системы.

При поступательном движении твердого тела теорема о движении центра масс дает дифференциальное уравнение , решение которого  полностью описывает движение твердого тела (так как здесь достаточно найти движение одной из точек тела и далее можно вычислить остальные характеристики движения тела).

При вращении тела около неподвижной оси теорема об изменении кинетического момента тела относительно неподвижной оси  дает уравнение

                    ,

решая которое получим зависимость угла поворота  и тем самым полностью определим вращательное движение тела.