 Пусть дано уравнение
Пусть дано уравнение ![]() Корнем этого уравнения
называется такое значение
Корнем этого уравнения
называется такое значение ![]() , при котором
, при котором ![]() Корень
Корень ![]() называется
простым, если
называется
простым, если ![]() , в против-
, в против-
ном случае - кратным. Целое число ![]() называется кратностью корня
называется кратностью корня ![]() , если
, если ![]() Геометрически
корень
Геометрически
корень ![]() соответствует точке пересечения графика
функции
соответствует точке пересечения графика
функции ![]() с осью
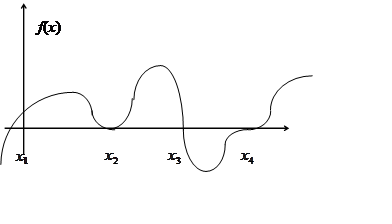
с осью ![]() Корень
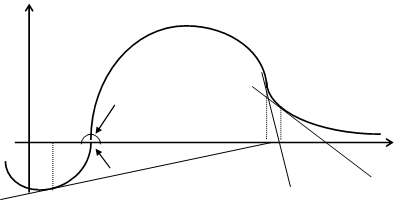
кратный, когда пересечение происходит под нулевым углом. На рисунке
Корень
кратный, когда пересечение происходит под нулевым углом. На рисунке ![]() ,
, ![]() -
простые корни,
-
простые корни, ![]() ,
, ![]() -
кратные. В подавляющем большинстве случаев представить решение уравнения
-
кратные. В подавляющем большинстве случаев представить решение уравнения ![]() в виде конечной замкнутой формулы оказывается
невозможным. Даже для простейшего
в виде конечной замкнутой формулы оказывается
невозможным. Даже для простейшего
алгебраического уравнения ![]() -й степени
-й степени ![]() явные формулы корней известны для
явные формулы корней известны для ![]() Уже для уравнения пятой (и более высоких
степеней) таких формул не существует.
Уже для уравнения пятой (и более высоких
степеней) таких формул не существует.
Задача отыскания корней нелинейного уравнения решается в два
этапа. Первый называется этапом локализации (отделения) корней, второй - этапом
итерационного уточнения корней. Отрезок ![]() ,
содержащий только один корень
,
содержащий только один корень ![]() уравнения
уравнения ![]() , называется отрезком локализации корня
, называется отрезком локализации корня ![]() . Способы локализации корней многообразны,
и указать универсальный метод не представляется возможным. Иногда отрезок
локализации известен либо он определяется из физических соображений. В простых
случаях хороший результат может дать графический метод. На этапе итерационного
уточнения корней с точностью
. Способы локализации корней многообразны,
и указать универсальный метод не представляется возможным. Иногда отрезок
локализации известен либо он определяется из физических соображений. В простых
случаях хороший результат может дать графический метод. На этапе итерационного
уточнения корней с точностью ![]() используют тот или иной
итерационный метод, позволяющий строить последовательность
используют тот или иной
итерационный метод, позволяющий строить последовательность ![]() приближений к корню
приближений к корню ![]() . Итерационный метод называют одношаговым,
если для вычисления очередного приближения
. Итерационный метод называют одношаговым,
если для вычисления очередного приближения ![]() используется
только одно предыдущее приближение
используется
только одно предыдущее приближение ![]() и
и ![]() - шаговым, если для вычисления
- шаговым, если для вычисления ![]() используется
используется ![]() предыдущих
приближений
предыдущих
приближений ![]() Столько же данных необходимо для
начального приближения, чтобы запустить метод.
Столько же данных необходимо для
начального приближения, чтобы запустить метод.
Скорость сходимости - одна из важнейших характеристик
итерационных методов. Говорят, что метод сходится со скоростью геометрической
прогрессии, знаменатель которой ![]() , если для
, если для ![]() справедлива оценка:
справедлива оценка:
![]() (6.1.1)
(6.1.1)
При определении скорости сходимости метода используют понятие порядка сходимости. Если справедливо неравенство
![]() (6.1.2)
(6.1.2)
то число ![]() называют
порядком сходимости. Если
называют
порядком сходимости. Если ![]() , то сходимость линейная
(сходимость геометрической прогрессии), при
, то сходимость линейная
(сходимость геометрической прогрессии), при ![]() сходимость
называется сверхлинейной. Если
сходимость
называется сверхлинейной. Если ![]() , скорость сходимости
называют квадратичной.
, скорость сходимости
называют квадратичной.
Если ![]() , то есть метод обладает
линейной сходимостью, можно установить справедливость формулы
, то есть метод обладает
линейной сходимостью, можно установить справедливость формулы
![]() ; (6.1.3)
; (6.1.3)
смотрите метод простых итераций или
метод Зейделя в предыдущей главе. Если же ![]() , то
справедлива оценка
, то
справедлива оценка
![]() (6.1.4)
(6.1.4)
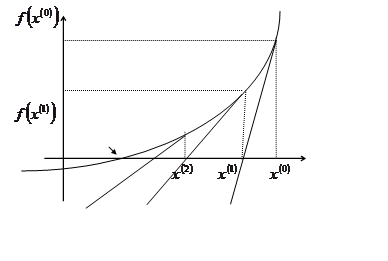 Этот знаменитый метод - один из наиболее эффективных методов решения
самых разных нелинейных задач. Выведем его расчетную формулу, исходя из
простейших геометрических соображений. Соответствующая иллюстрация приведена на
рисунке слева. Пусть
Этот знаменитый метод - один из наиболее эффективных методов решения
самых разных нелинейных задач. Выведем его расчетную формулу, исходя из
простейших геометрических соображений. Соответствующая иллюстрация приведена на
рисунке слева. Пусть
![]() - заданное начальное условие. В точке
- заданное начальное условие. В точке ![]() с координатами
с координатами ![]() проведем
касательную к графику функции
проведем
касательную к графику функции ![]() и за новое приближение
и за новое приближение ![]() примем абсциссу точки пересечения этой
касательной с осью
примем абсциссу точки пересечения этой
касательной с осью ![]() Далее поступают аналогично, за
приближение
Далее поступают аналогично, за
приближение ![]() берут абс
берут абс![]()
![]() циссу точки пересечения с осью
циссу точки пересечения с осью ![]() касательной,
проведенной к графику в точке
касательной,
проведенной к графику в точке ![]() и так далее. Уравнение
касательной, проведенной к графику
и так далее. Уравнение
касательной, проведенной к графику ![]() в точке
в точке ![]() , имеет вид
, имеет вид ![]() . Если
положить здесь
. Если
положить здесь ![]() , тогда абсцисса точки
, тогда абсцисса точки ![]() пересечения касательной с осью
пересечения касательной с осью ![]() будет удовлетворять этому уравнению, то
есть
будет удовлетворять этому уравнению, то
есть ![]() Отсюда
Отсюда
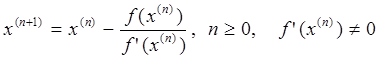 . (6.2.1)
. (6.2.1)
Это и есть основная рабочая формула метода Ньютона или метода касательных, получившего свое второе название благодаря указанной геометрической интерпретации.
Теорема 6.1. Пусть ![]() -
простой корень уравнения
-
простой корень уравнения ![]() , в некоторой окрестности
которого функция
, в некоторой окрестности
которого функция ![]() дважды непрерывно
дифференцируема. Тогда найдется такая малая
дважды непрерывно
дифференцируема. Тогда найдется такая малая ![]() -окрестность
корня
-окрестность
корня ![]() , что при произвольном выборе начального приближения
, что при произвольном выборе начального приближения
![]() из этой окрестности итерационная
последовательность метода Ньютона не выходит за пределы этой окрестности и
справедлива оценка
из этой окрестности итерационная
последовательность метода Ньютона не выходит за пределы этой окрестности и
справедлива оценка
![]() (6.3.1)
(6.3.1)
где ![]() . Это
означает, что метод Ньютона сходится с квадратичной скоростью. Грубо говоря, на
каждой итерации число верных знаков приближения примерно удваивается.
. Это
означает, что метод Ньютона сходится с квадратичной скоростью. Грубо говоря, на
каждой итерации число верных знаков приближения примерно удваивается.
 Простота и высокая скорость сходимости
делает метод Ньютона чрезвычайно привлекательным. Однако имеются две существенные
трудности. Первая из них - необходимость вычисления производной
Простота и высокая скорость сходимости
делает метод Ньютона чрезвычайно привлекательным. Однако имеются две существенные
трудности. Первая из них - необходимость вычисления производной ![]() Это часто либо невозможно
Это часто либо невозможно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.