


















21.  22.
22. 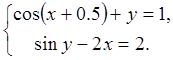
23. 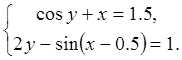 24.
24. 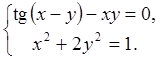
25. 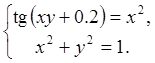 26.
26. 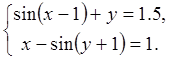
27. 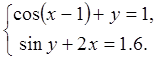 28.
28. 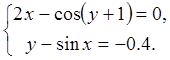
29. 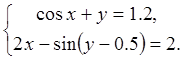 30.
30. 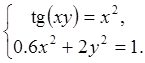
Большая часть инженерных задач приводит к законам и правилам, которые формулируются в виде дифференциальных уравнений. Основная задача, решаемая для таких уравнений, - это задача Коши или начальная задача. В подавляющем большинстве случаев она решается с использованием вычислительной техники. Рассмотрим методы решения дифференциальных уравнений первого порядка.
Решением обыкновенного
дифференциального уравнения первого порядка ![]() называется
функция
называется
функция ![]() , обращающая это уравнение в тождество при
подстановке. График решения называется интегральной кривой.
, обращающая это уравнение в тождество при
подстановке. График решения называется интегральной кривой.
![]()
![]()


![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
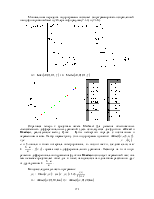
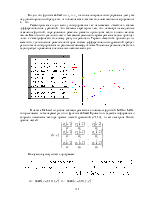
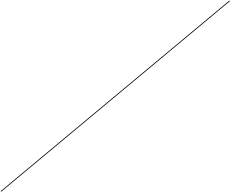
На рисунке справа изображено поле направлений, представляющее семейство интегральных кривых уравнения
![]() . (7.1.1)
. (7.1.1)
Задание начального условия - точки ![]() выделяет из этого семейства конкретную кривую,
дающую частное решение уравнения (7.1.1).
выделяет из этого семейства конкретную кривую,
дающую частное решение уравнения (7.1.1).
Задача нахождения при ![]() решения
решения ![]() дифференциального
уравнения (7.1.1), удовлетворяющего начальному условию
дифференциального
уравнения (7.1.1), удовлетворяющего начальному условию
![]() (7.1.2)
(7.1.2)
называется задачей Коши. Чаще
всего решение ищут на конечном заданном отрезке ![]() .
.
Теорема 7.1. (Теорема
существования и единственности решения). Пусть функция ![]() определена
и непрерывна в области
определена
и непрерывна в области ![]() и удовлетворяет в ней условию
Липшица*
по переменной
и удовлетворяет в ней условию
Липшица*
по переменной ![]() , то есть
, то есть
![]() (7.1.3)
(7.1.3)
Тогда для любого начального
значения ![]() существует единственное решение
существует единственное решение ![]() задачи Коши с заданным начальным условием
задачи Коши с заданным начальным условием
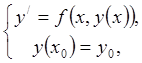
определенное на отрезке ![]()
На практике для дифференцируемых
по ![]() функций
функций ![]() условие(7.1.3) заменяется более грубым условием
условие(7.1.3) заменяется более грубым условием
![]() (7.1.4)
(7.1.4)
то есть условием ограниченности частной производной.
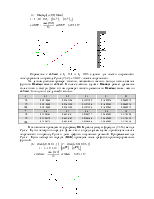
Численное решение задачи Коши строится для ее дискретного
аналога. В этом случае отрезок ![]() - область непрерывности
изменения аргумента
- область непрерывности
изменения аргумента ![]() заменяется множеством
заменяется множеством
![]() - конечным множеством точек
- конечным множеством точек ![]() , которое называется сеткой. Величина
, которое называется сеткой. Величина ![]() - шаг сетки - является, как правило,
постоянным, то есть сетки в большинстве случаев равномерные.
- шаг сетки - является, как правило,
постоянным, то есть сетки в большинстве случаев равномерные.
Функции, определенные лишь в узлах сетки ![]() , называются сеточными. Они помечаются
индексом
, называются сеточными. Они помечаются
индексом ![]() , например,
, например, ![]() , чаще
же значение функции
, чаще
же значение функции ![]() в узлах сетки
в узлах сетки ![]() обозначается обычным образом с помощью
индекса, например,
обозначается обычным образом с помощью
индекса, например, ![]() или
или ![]()
В основе построения конкретного численного метода лежит тот
или иной способ замены дифференциального уравнения ![]() его
дискретным аналогом - уравнением вида
его
дискретным аналогом - уравнением вида
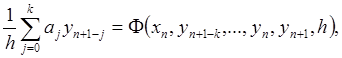 (7.2.1)
(7.2.1)
где ![]() -
значения сеточной функции в
-
значения сеточной функции в ![]() последовательных точках
последовательных точках
![]() Сумма в левой части формулы (7.2.1)
рассматривается как разностная аппроксимация производной
Сумма в левой части формулы (7.2.1)
рассматривается как разностная аппроксимация производной ![]() по одной из формул численного
дифференцирования, а правая часть - как специальным
образом построенная аппроксимация функции
по одной из формул численного
дифференцирования, а правая часть - как специальным
образом построенная аппроксимация функции ![]() .
.
При нахождении приближения ![]() в очередной точке сетки по формуле (7.2.1)
используются найденные ранее значения сеточной функции
в очередной точке сетки по формуле (7.2.1)
используются найденные ранее значения сеточной функции ![]() в
в
![]() предыдущих точках
предыдущих точках ![]() .
Такие методы называются
.
Такие методы называются ![]() -шаговыми. При
-шаговыми. При ![]() уравнение (7.2.1) принимает вид
уравнение (7.2.1) принимает вид
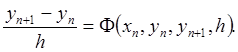 (7.2.2)
(7.2.2)
Соответствующий этой формуле метод
называется одношаговым. Вычисление ![]() осуществляется здесь с
использованием только одного предыдущего значения
осуществляется здесь с
использованием только одного предыдущего значения ![]() .
.
В случае, когда входящая в уравнение (7.2.1) функция ![]() не зависит от
не зависит от ![]() , вычисление
, вычисление
![]() не вызывает затруднений и осуществляется
по явной формуле
не вызывает затруднений и осуществляется
по явной формуле
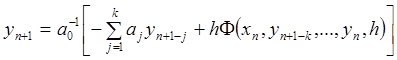 . (7.2.3)
. (7.2.3)
Соответствующие методы называются
явными. Напротив, если ![]() зависит от
зависит от ![]() , на каждом шаге приходится решать
относительно
, на каждом шаге приходится решать
относительно ![]() нелинейное уравнение (7.2.1). Методы, реализующие
такой алгоритм, называются неявными.
нелинейное уравнение (7.2.1). Методы, реализующие
такой алгоритм, называются неявными.
Начнем с метода, который теоретически пригоден для решения любых дифференциальных уравнений, но с вычислительной точки зрения не представляет почти никакого практического интереса. Его ценность заключается в том, что он дает некоторый эталон для сравнения различных практически удобных методов.
Запишем разложение функции ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() :
:
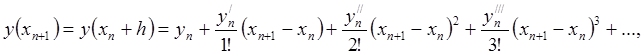 (7.3.1)
(7.3.1)
где ![]() есть
есть ![]() -я производная функции
-я производная функции ![]() в точке
в точке ![]() Пусть
имеется приближенное решение уравнения (7.3.1) для
Пусть
имеется приближенное решение уравнения (7.3.1) для ![]() точки
точки ![]() Найдем приближенное решение для точки
Найдем приближенное решение для точки ![]() , подставив
, подставив ![]() в
формулу (7.3.1). Получим
в
формулу (7.3.1). Получим
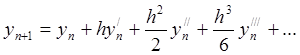 (7.3.2)
(7.3.2)
Чем больше членов ряда (7.3.2) взять
для вычислений, тем точнее будет приближение. В любом случае необходимо
вычислять различные производные функции ![]() . Из
(7.1.1) имеем
. Из
(7.1.1) имеем ![]() Дифференцируя по
Дифференцируя по ![]() , получим
, получим
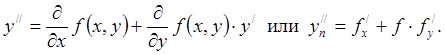 (7.3.3)
(7.3.3)
При этом уравнение (7.3.2) приобретает вид
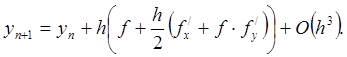 (7.3.4)
(7.3.4)
Процедура нахождения решения с помощью ряда Тейлора является
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.