Метод простой итерации. Алгоритм вычисления корня уравнения методом простой итерации в Microsoft Excel

Метод простой итерации

Пусть дано уравнение f(x)=0 и в интервале (a,b) существует корень. Из (a,b) выбирается начальное значение x₀.

При уточнении корня методом простой итерации уравнение приводится к виду:

                                    (1)

Где  - некоторая функция от x.

Если функция  и ее производная  непрерывны на всем интервале поиска корня, то при выполнении условия

                                 (2)

метод простых итераций сходится.

Из интервала [a,b] выбирается начальное приближение x₀, подставляется в уравнение (1) и получается новое приближение . По аналогии находится второе приближение  и так далее, наконец,

                                (3).

Критерий окончания итерационного процесса имеет вид:

.                             (4)

Численный пример

Рассмотрим функцию . Один из промежутков локализации [0,3;1]. Вычислить корень уравнения с точностью . Определить количество итераций.

Приведем уравнение к виду (1). , отсюда .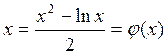

Найдем производную .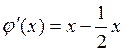

Пусть начальное приближение x₀=1, тогда . Условие сходимости метода (2) выполняется.

Определяем .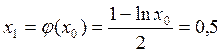

Вычисляем . Так как модуль разности двух приближений больше ε, то вычисляем следующее значение x₂.

.

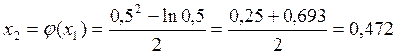Вычисляем , поэтому вычисляем

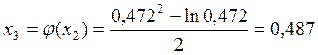 и т.д.

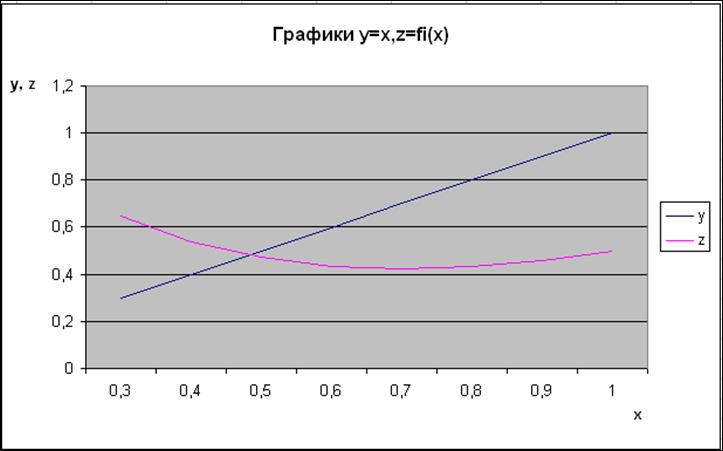
Ниже приводится алгоритм вычисления корня уравнения методом простой итерации: