Ways of representation of the algorithm the controlling automaton follows, страница 4

            If there are no transition from an operator to another, the cell of the table is left empty.

            It is easy to obtain the MSA from the GSA. Build up the table, consider all possible transitions from an operator to others, write down the conditions of transitions a_ij in the cells.

            Each the row of the matrix has to satisfy the conditions:

a)                b)                    (26.1)

            Aided with the condition (26.1a)), fullness of the automaton definition is determined.

The condition (26.1b)) determines consistency of the algorithm definition with the MSA. If it isn’t satisfied, there are some ways to continue an algorithm (to execute some operators simultaneously), but it is contrary to the algorithm definition.

26.3 The system of transition formulas

            Look at the Fig. 26.4. The fact it is possible to execute the operators Y₂,Y₃ and Y₄ after the operator Y₂ can be denoted in a form of formula:

           

            Let’s denote the logic conditions in such a way:

           

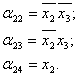
            In the general case, the transition from an operator is determined by the formula (26.2):

            ,                           (26.2)

            where a_ij is a boolean function of transiting from an operator Y_i to the operator.

            The expression  is called the marked boolean function. The marked boolean function gains the values respectively the rule (26.3):

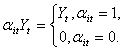                 (26.3)

The marked boolean functions may be applied the laws of the boolean algebra.

For example, the next transformations hold true:

                                   (26.4)