Кратчайшие пути для всех пар вершин взвешенного ориентированного графа

Кратчайшие пути для всех пар вершин взвешенного ориентированного графа.

Задача нахождения кратчайших путей из всех вершин формирует таблицу весов, в которой на пересечении строки i и столбца j, находится вес кратчайшего пути из iвjинформация о самом пути.

Эту задачу можно решить для орграфа G = (V, E) с заданной весовой функцией w: EàR если |V| раз применить алгоритм поиска кратчайших путей для всех вершин поочередно. Если ребра имеют неотрицательные веса, то можно применить алгоритм Дейкстры. Общее время алгоритма составит O(V(V²+E)) = O(V³) или O(VE log V), если в алгоритме Дейкстры используется очередь с приоритетами. Для разреженных графов это вполне допустимо.

Если в орграфе есть ребра с отрицательным весом, то можно использовать более медленный алгоритм Беллмана - Форда и общее время составит O(V²E) а для плотных графов O(V⁴).

Изобретены более быстрые алгоритмы. Наиболее удобны эти алгоритмы для орграфов, представленных матрицами. Исходными данными для этих алгоритмов является матрица весов взвешенного орграфа W = (w_ij) элементы равны:

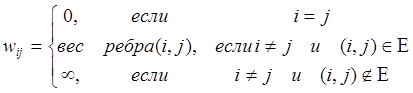Веса ребер могут быть отрицательными, но предполагается, что циклов отрицательного веса в орграфе нет.

Алгоритм формирует матрицу D = (d_ij), элементы которой d_ij = d(i, j) (вес кратчайшего пути). Кроме того, формируется матрица предшествования P =(p_ij), в которой p_ij является вершиной

предшествующей вершине j на одном из кратчайших путей из i            j. p_ij = NIL для i = j или, если пути из  i  в  j нет. Для каждой вершины iÎV можно выделить подграф предшествования       G_{p, i} = (V_{p, i}, E_{p, i}),  где V_{p, i}, = {jÎV: p_ij ¹ NIL} È {i}

                                     E_{p, i}, = {(p_ij, j): jÎ V_{p, i}, и p_ij ¹ NIL}.

Имея такую матрицу, можно построить путь из вершины i в j:

All_Pathes(P, i, j)

1.  if i = j

2.     then печать i

3.     else  if  p_ij = NIL

4.                  then печать "пути из i в j нет"

5.                  else All_Pathes(P, i, p_i,j )

6.                         печать j

Алгоритм Флойда – Уоршолла.

Алгоритм Флойда - Уоршолла является алгоритмом динамического программирования. Алгоритм допускает ребра с отрицательным весом, но не допускает циклы с отрицательным весом.

Строение кратчайшего пути.

Введем понятие промежуточной вершины: если есть простой путь p = <v₁, v₂, ..., v_i >, то вершины v₂, v₃, ... v_i-1 называются промежуточными.

Для простоты будем обозначать вершины графа G числами 1, 2,..., n. Рассмотрим подмножество вершин k £ n. Для каждой пары вершин i, j Î V рассмотрим все пути из i, j включающие в путь только вершины {1, 2,...,k}.

Среди них можно выделить путь с минимальным весом. Вес этого пути можно получить, зная вес минимального пути между i, j, включающего вершины {1, 2,...,k-1}.

При добавлении вершины k между вершинами i и j, новый минимальный путь может содержать вершину k в качестве промежуточной или нет.

Если вершина k не вошла в минимальный путь, то новый минимальный путь включает в себя минимальный путь для множества {1, 2,...,k-1}.

Если вершина k промежуточная, то новый минимальный путь разбивается на 2 участка.

Минимальные пути p₁ и p₂ включают в себя вершины {1, 2, ..., k-1}, которые также должны быть минимальны.

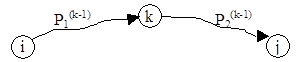Исходя из этих рассуждений, можно выделить рекуррентное соотношение между решениями подзадач.

Пусть d _ij ^(k) - вес кратчайшего пути из вершины i в j с промежуточными вершинами из подмножества {1, 2,...,k}.

При k = 0прормежуточных путей нет и d _ij ⁽⁰⁾ =w_ij

В общем случае:

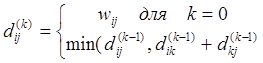Матрица D⁽ⁿ⁾ = d⁽ⁿ⁾_ij содержит искомое решение, т. е. d⁽ⁿ⁾_ij=d(i, j) для всех i, j Î V, т. к. разрешены любые промежуточные вершины.

Помимо весов кратчайших путей параллельно в матрице p фиксируются p^(k)_ij

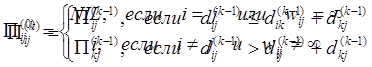Вычисление кратчайших путей снизу вверх.

Входом алгоритма является матрица весов, результатом - матрица весов кратчайших путей D⁽ⁿ⁾.

Floyd_Warshall (W)

1.  n← |V[G]|

2.  D⁽⁰⁾ ←W

3.  for i←1 to n

4.  for j←1 to n

5.        if (w_ij¹¥) then p_ij←i

6.                                p_ii←nil

7.             else p_ii←nil

8.  for k←1 to n

9.        do for i←1 to n  

10.             do for j←1 to n  

11.                  do if (^d(k)_ij) ←min (d^(k-1)_ij, d^(k-1)_ik + d^(k-1)_kj)

12.  return D⁽ⁿ⁾

Пусть дан граф:

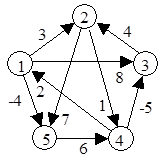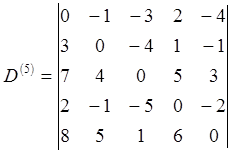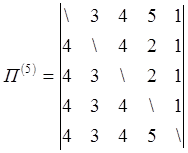
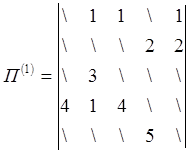
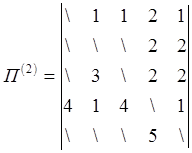
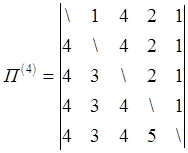
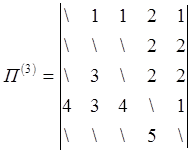
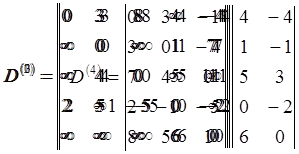Транзитивное замыкание орграфа.

Задача о транзитивном замыкании состоит в следующем: дан орграф G=(V, E) с вершинами 1,  2, ...,n. Требуется определить для любой пары вершин i, j ÎV существует ли в графе путь из вершины i в вершину j. Транзитивным замыканием орграфа G называется орграф G^*=(V, E), где E^*={(i, j): в графе G  существует путь из i в j}. Транзитивное замыкание можно вычислять за время O(n³) при помощи алгоритма Флойда - Уоршолла считая, что все ребра имеют вес 1. В результате d_ij<n, если между вершинами i и j существует путь, или d_ij=¥, если между вершинами i и j пути нет. Для решения задачи используется модифицированный алгоритм Флойда - Улршолла. В нем операции “min” и “+” заменяются на логические операции И (Ù) и ИЛИ (Ú). Положим t^(k)_ij=1, если в графе G существует путь из i в j с промежуточными вершинами из множества {1, 2,...,k} и t^(k)_ij=0, если такого пути нет. Ребро (i, j) принадлежит транзитивному замыканию G^* тогда и только тогда, когда t⁽ⁿ⁾_ij=1.