Среднеквадратичная аппроксимация функций

         Среднеквадратичная аппроксимация функций предполагает интегральную близость между приближаемой и приближающей функциями на интервале аппроксимации, что существенно расширяет класс приближаемых функций, не накладывая требования их непрерывности. Достаточно, чтобы приближаемая функция была интегрируема со своим квадратом на интервале аппроксимации, т.е. чтобы .

         Кроме того, в ряде случаев просто нет необходимости требовать близости в каждой точке интервала , т.е. требовать равномерного приближения.

            Целесообразность среднеквадратичной аппроксимации можно объяснить еще и с практических позиций. Приближаемая , как правило, задана таблично, причем значения получены экспериментально, а следовательно, содержит случайные погрешности и приближающая функция, полученная методом среднеквадратичной аппроксимации лучше представляет реальную за счет сглаживающих свойств (усреднения) интегрального оператора, имеющего место при определении коэффициентов аппроксимирующей функции.

2. Постановка задачи

На интервале  произвести аппроксимацию реализации функции , заданной на  с шагом  (в таблице функция  приведена в аналитическом виде), обобщенным рядом Фурье по системе ортогональных (ортонормированных) на  с весом  базисных функций .

Определить на  погрешности аппроксимации.

Проанализировать влияние числа  учитываемых членов ряда Фурье на точность аппроксимации изменяя параметр  от  до с шагом .

3. Теоретические положения

Произвольную, кусочно-непрерывную функцию   на  интервале  приближенно можно представить в виде обобщенного ряда Фурье с конечным числом членов

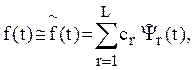                                                                                                         (1.1)

где , - система ортогональных с весом  на  базисных функций, а

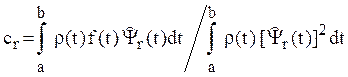                                       (1.2)

коэффициенты Фурье.

Таким образом, чтобы решить задачу аппроксимации функции   на  , необходимо при заданном базисе , вычислить коэффициенты Фурье  согласно (1.2) и восстановить оценку  аппроксимируемой функции  по выражению (1.1).

В качестве базисной функции используются полиномы Чебышева.

Полиномы Чебышева первого рода, ортогональные на   с весом 

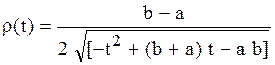                                                                                             (1.6)

также могут вычисляться по рекуррентной формуле:

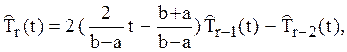                                                                (1.7)

          .          

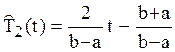Нормирующий множитель  полиномов Чебышева первого рода

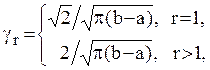                                                                                               (1.8)

а ортонормированные полиномы Чебышева первого рода определяются в виде

                                                            .                                                            (1.9)

При вычислении на ЭВМ коэффициентов  ряда Фурье по полиномам Чебышева в моменты времени t = a  и  t = b подкоренное выражение в весовой функции  обращается в нуль. Чтобы избежать операции деления на нуль, в подкоренное выражение можно ввести  некоторый малый параметр  (например , где  - шаг дискретизации). Однако введение параметра  приводит к дополнительной погрешности в вычислениях коэффициентов Фурье, что в конечном итоге сказывается на погрешности аппроксимации. Причем, как показывает практика, погрешности, порожденные параметром , оказываются соизмеримыми с погрешностями от отбрасывания остаточного члена ряда Фурье при L = 3, 4 при аппроксимации на  полупериода синусоиды.

Точность аппроксимации   на  обобщенным рядом Фурье  следует оценивать посредством следующих погрешностей:

- максимальной на  абсолютной и относительной

     ;                                       (1.15)

- среднеквадратичной на  абсолютной и относительной

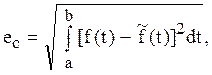
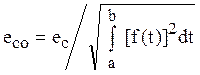     .                                 (1.16)

4. Листингпрограммы.

        real f(147),t(147),ro(147),th(7,147),f1(147),c(7),ff(147)

        real a,b,dt,e(147),em,es,ep,emo,eso,epo,ff1(147),ff2(147)

        real ff3(147)

        integer i,kon,l

        open (1,file='1.dat')

        a=1.05

        b=4.7

        dt=0.025

        kon=(b-a)/dt+0.2

        do 1 i=1,kon

        t(i)=a+dt*(i-1)

        f(i)=4-2*cos(t(i))

1       continue

        open (4,FILE='3.gra')

        do 2 l=3,7

        call n1ypth(a,b,kon,dt,l,ro,th)

        call n1ykf(kon,dt,l,f,f1,th,ro,c)

        call n1ywst(kon,l,c,th,ff)

        call n1yeee(f,ff,kon,e,em,es,ep,emo,eso,epo)

        write (4,*)l,emo,eso

        write (1,11)

        write (1,10)l

        write (1,16)

        write (1,12)

        do 4 i=1,l

        write (1,13) i,c(i)

4       continue

        write (1,14) l-2,l

        do 3 i=1,kon

        if ((l.eq.4).or.(l.eq.6)) go to 7

        if (l.eq.3) ff1(i)=ff(i)

        if (l.eq.5) ff2(i)=ff(i)

        if (l.eq.7) ff3(i)=ff(i)

7       write (1,15) t(i),f(i),ff(i),e(i)

3       continue

2       continue

        close(4)

        l=5

        write (1,11)

        write (1,17)

        write (1,19)

        open (3,FILE='2.gra')

        do 5 i=1,kon

        write (1,18) t(i),(th(j,i),j=1,5)

        write (3,*)t(i),ro(i),(th(j,i),j=1,5)

5       continue

        close (3)

        write (1,11)

        write (1,20)

        write (1,21)

        do 6 i=1,kon

        write (1,22)t(i),ro(i)

6       continue

        close (1)

        open(2,FILE='1.gra')

        do 8 i=1,kon

        write (2,*)t(i),f(i),ff1(i),ff2(i),ff3(i)

8       continue

        close(2)

10      format ('Число учитываемых членов ряда Фурье:',I1)

11      format (1x/'───────────────────────────────────────────')

12      format ('Коэффициенты Фурье:')

13      format ('c(',I1,')=',f11.8)

14      format (1x/'Табл.',1x,I1/8x,'Результаты расчетов при l=',I1/3x,

     *  'T',9x,'F',10x,'~F',10x,'E')

15      format (f6.3,1x,f11.8,1x,f11.8,1x,f11.8)

16      format (1x)

17      format (1x/'Табл. 6'/11x,

     *  'Реализации первых пяти базисных функций')

18      format (F6.3,1x,f11.8,1x,f11.8,1x,f11.8,1x,f11.8,1x,f11.8)

19      format (3x,'T',8x,'^T1',9x,'^T2',9x,'^T3',9x,'^Т4',9x,'^T5')

20      format (1x/'Табл. 7'/'Реализация весовой функции')

21      format (6x,'T',8x,'Po')

22      format (3x,F6.3,1x,f11.8)

        end

Аппроксимированные на заданном интервале  значения для  от  до , а также значения базисной функции и коэффициентов Фурье выводятся во внешние файлы. Для реализации базисной функции Чебышева используется процедура N1YPЕР, коэффициенты ряда вычисляются в N1YKF. Восстановление оценки аппроксимируемой функции производится процедурой N1YWST. Наконец, погрешности аппроксимации оцениваются в N1YEEE. Вычисления и вывод результатов происходит в цикле отражающим количество учитываемых членов ряда Фурье.

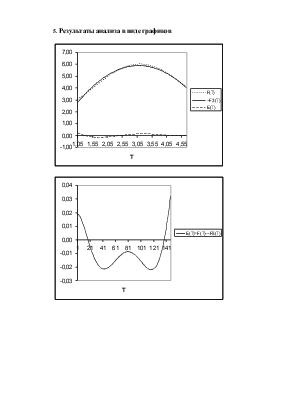
5. Результаты анализа в виде графиков

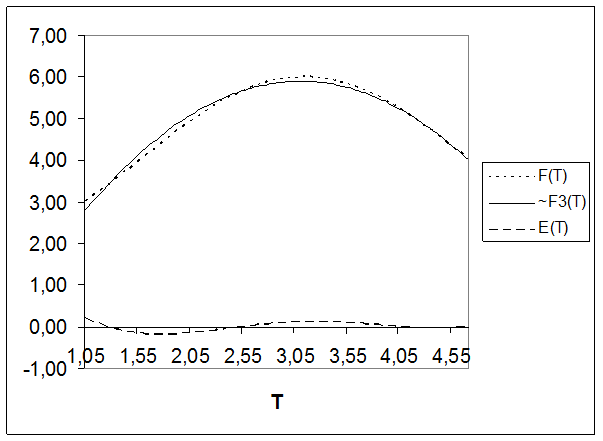
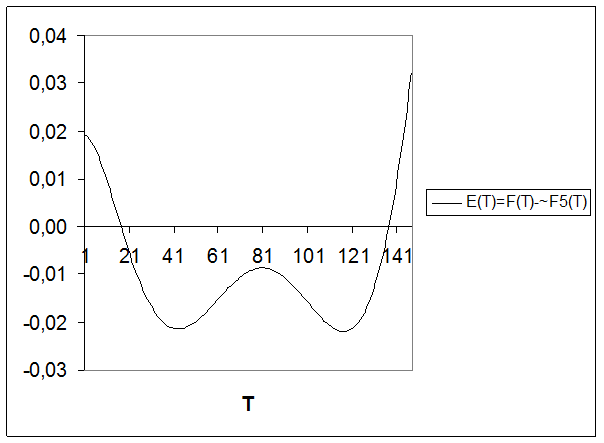
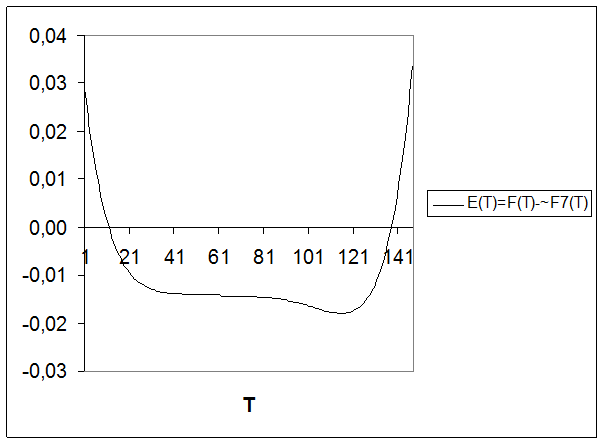
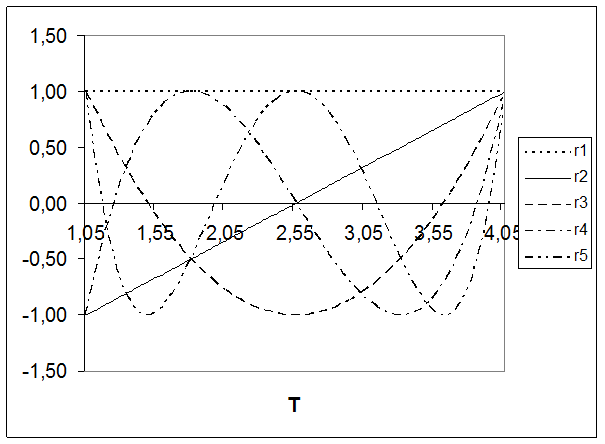
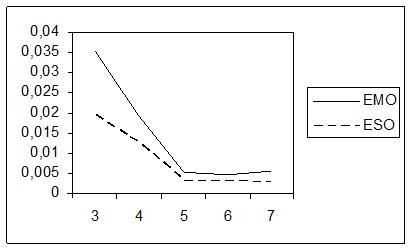
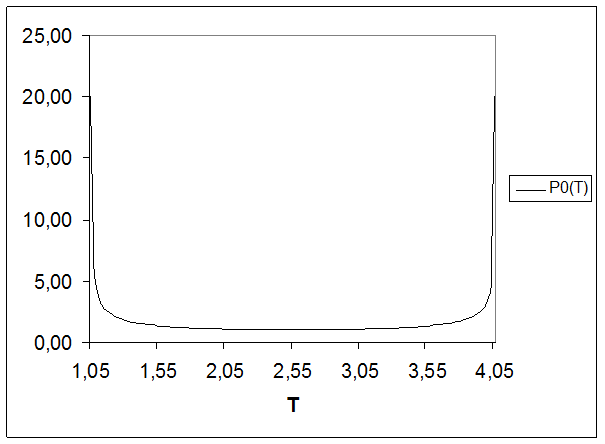
6. Заключение

            Аппроксимировали заданную функцию в соответствии с вариантом обобщенным рядом Фурье по системе ортогональных (ортонормированных) базисных