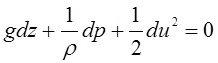 . (3.78)
. (3.78)
Разделим
все слагаемые уравнения на ускорение свободного падения ![]() ,
тогда получим
,
тогда получим
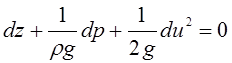 . (3 79)
. (3 79)
Приращение суммы всех трех членов этого уравнения при перемещении вдоль линии тока равно нулю.
Проинтегрировав дифференциальное уравнение (3.79), получим
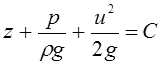 . (3.80)
. (3.80)
Сумма всех членов вдоль линии тока жидкости - величина постоянная, а следовательно, и вдоль идеальной элементарной струйки она также постоянна.
Уравнение (3.80), полученное с помощью уравнения движения Эйлера, для установившегося движения является уравнением Бернулли. Идентичное уравнение было получено ранее иным путем с использованием теоремы кинетической энергии (3.43).
Уравнение (3.80), записанное для двух живых сечений струйки, приобретает известный ранее вид
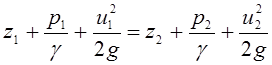 .
.
3.10. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА РЕАЛЬНОЙ ЖИДКОСТИ
Рассмотрим участок потока реальной жидкости, ограниченный по поверхности непроницаемыми стенками. Такой ноток называется потоком конечных размеров (рис. 3.10). Поток жидкости представляет собой совокупность множества элементарных струек. Движение струек является установившимся, т.е. скорость в любом сечении струйки по длине постоянна. На струйку действуют только силы тяжести.
В начале участка (сечение 1-1) и в конце (сечение 2-2) движение жидкости будем считать плавно изменяющимся или параллельно струйным.
Уравнение Бернулли для реальной струйки
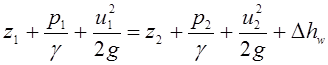 .
.
Умножим
все члены уравнения на единицу веса жидкости, протекающей через живое сечение
струйки за время ![]() .
.
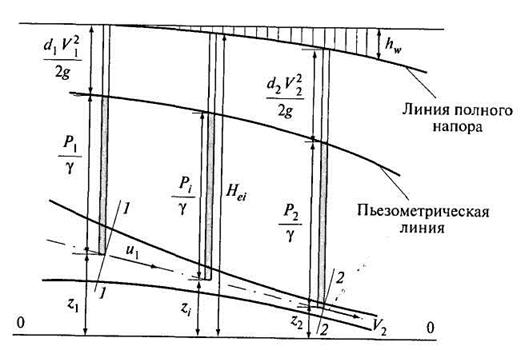
Рис. 3.10. К уравнению Бернулли для потока реальной жидкости
Единица веса части струйки
![]() . (3.81)
. (3.81)
В
результате умножения получим сумму потенциальной и кинетической энергий в
сечениях 1-1 и 2-2 за время ![]() , т.е.
мощность струйки в сечениях:
, т.е.
мощность струйки в сечениях:
 . (1.82)
. (1.82)
Так как
поток состоит из множества струек, то можно проинтегрировать уравнение (3.82)
по живым сечениям потока жидкости ![]() , и
, и ![]() :
:
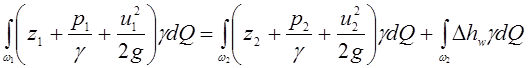 , (3.83)
, (3.83)
где 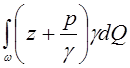 потенциальная энергия, отнесенная к
единице времени.
потенциальная энергия, отнесенная к
единице времени.
Для
плавно изменяющегося или параллельноструйного движения жидкости для разных
точек определенного поперечного сечения гидростатический напор 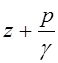 является постоянной величиной, тогда
является постоянной величиной, тогда
 , (3.84)
, (3.84)
где 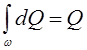 ;
; 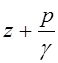 - удельная потенциальная энергия,
принимается относительно центра тяжести живого сечения потока конечных
размеров;
- удельная потенциальная энергия,
принимается относительно центра тяжести живого сечения потока конечных
размеров; ![]() - расстояние от центра тяжести сечения до
плоскости сравнения 0-0.
- расстояние от центра тяжести сечения до
плоскости сравнения 0-0.
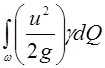 - кинетическая энергия, отнесенная к единице времени.
- кинетическая энергия, отнесенная к единице времени.
Действительная кинетическая энергия
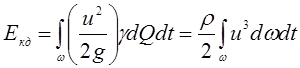 . (3.85)
. (3.85)
Действительная кинетическая энергия потока реальной жидкости соответствует реальному распределению местных скоростей по сечению. На рис. 3.11 изображено распределение в трубе скоростей действительного потока. Скорости в разных точках сечения трубы являются переменными величинами.
Как уже отмечалось ранее, для упрощения гидравлических расчетов используется понятие средней скорости течения жидкости V. Используя среднюю скорость при определении кинетической энергии, получим условную кинетическую энергию потока в сечении. Условная кинетическая энергия
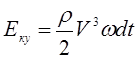 . (3.86)
. (3.86)
Условной
кинетической энергии соответствует прямоугольная эпюра (см. рис. 3.11), где ![]() по сечению трубы. Условная кинетическая
энергия меньше действительной,
по сечению трубы. Условная кинетическая
энергия меньше действительной, ![]() .
.
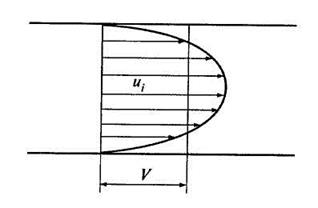
Рис. 3.11. Распределение скоростей
Разделим выражение (3.85) на (3.86), получим
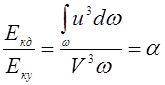 , (3.87)
, (3.87)
где ![]() -
безразмерный поправочный коэффициент, коэффициент кинетической энергии.
-
безразмерный поправочный коэффициент, коэффициент кинетической энергии.
Коэффициент
![]() учитывает неравномерность распределения
скоростей в плоскости живого сечения потока. Действительная кинетическая
энергия
учитывает неравномерность распределения
скоростей в плоскости живого сечения потока. Действительная кинетическая
энергия
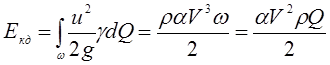 . (3.88)
. (3.88)
Чем
больше неравномерность распределения местных скоростей ![]() по
живому сечению потока, тем больше значение
по
живому сечению потока, тем больше значение ![]() .
.
В
результате проведения экспериментов было установлено, что при равномерном
движении турбулентного потока ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.