4. Расчеты на ЭВМ. На атом этапе отлаженная программа запускается на выполнение, осуществляется ввод числовых исходных данных и получается конечный результат, который при необходимости может быть представлен в удобной для пользователя форме, например в виде таблиц или графиков.
Решаемая задача может характеризоваться параметрами любой физической природы (температура, давление, механическое перемещение и т.д.), следовательно, исходные данные, вводимые в память ЭВМ, должны быть преобразованы соответствующими датчиками в электрические величины. Датчики - это приборы определенного класса точности и преобразования всегда осуществляются с некоторой погрешностью, которая является неустранимой и присутствует всегда, независимо от способа решения задачи. Такая погрешность называется погрешностью задания исходных данных.
5. Анализ полученных результатов. Наличие перечисленных выше погрешностей приводит к тому, что полученный результат может оказаться весьма далеким от истинного и его анализ потребует уточнения решения. Существует два основных пути повышения точности. Один из них - уточнение математической модели, что требует дополнительного изучения физической проблемы и приводит к существенному усложнению постановки задачи, а потому представляется менее целесообразным, чем второй - выбор другого, более точного алгоритма решения задачи. Иногда прибегают к расчетам на ЭВМ с удвоенной точностью, что уменьшает вычислительную погрешность.
2 Погрешности в вычислительной математике
Анализ влияния погрешностей на конечный результат позволяет дать следующие практические рекомендации по их соотношению. Методическая погрешность должна быть меньше неустранимой (погрешности несоответствия математической модели и задания исходных данных), а вычислительная погрешность меньше методической. При этом желательно, чтобы они были примерно одного порядка, поскольку очень существенное отличие приводит к неоправданным затратам машинного времени и ресурсов ЭВМ.
Наличие в общем случае погрешностей:
- несоответствия математической модели,
- задания исходных данных,
- методической,
- вычислительной -
приводит к результирующей погрешности решения. Поэтому вычислительная задача будет решена более полно, если удастся оценить точность, с которой найдено решение, т.е. ответить на вопрос - насколько полученный результат близок к истинному. Однако понятие близости можно трактовать различными способами, что определяется функциональными пространствами, в которых рассматриваются сравниваемые элементы. Ограничимся двумя функциональными пространствами.
Пространство
,включает в себя
множество непрерывных и дифференцируемых на интервале [a,b] функций. Расстояние 
между
элементами 
(функциями
) в
данном пространстве определяется в виде
а нормой функции f(x)
является
Говорят, что в пространстве 
последовательность
функций
,i=0,1,2,... сходится к f(x), если
причем эта сходимость называется равномерной.
Таким образом, если f(x) - истинное решение, а
-
приближенное, то близость между ними в равномерном смысле можно определить в
виде максимальной
(1)
и максимальной относительной
(2)
погрешностей, которые при расчетах на ЦВМ удобнее использовать в следующем виде
, (3)
, (4)
где 
представляют собой дискретные
отсчёты функции 
фиксированные на [а, b] с шагом
точке.
Пространству L2[а,b] принадлежат функции, интегрируемые со своим квадратом, т.е. такие, что
Расстояние между элементами 
в
пространстве 
определяется в виде:
а норма функции f(x) -
Если имеет место
то последовательность функций 
сходится
к f(x) на [a, b] в среднем (среднеквадратичная сходимость).
Среднеквадратичная погрешность между 
будет определяться как
, (5)
а среднеквадратичная относительная -
(6)
или в дискретном варианте для 
Рис.1
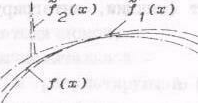x
a b
В качестве примера на рис.1 приведены функции
, близкая к f(x) в равномерном смысле, и 
,
близкая к f(x) в среднем.
3 Корректность постановки вычислительной задачи
Вычислительная задача называется корректно поставленной если:
1) решение существует,
2) решение единственное,
3) решение устойчивое (при вариации исходных данных).
Если хотя бы одно из этих положений нарушено, то задача будет поставлена некорректно.
Когда решения не существует, оно и не может быть найдено.
Примером существования неединственного решения может служить определение корней системы линейно зависимых алгебраических уравнений. При этом, используя, например, правило Крамера для решения такой системы, получают неопределенность типа О/О, и в качестве решения можно брать любые корни.
Решение является устойчивым, если небольшие изменения в исходных данных не приводят к большим отклонениям в решении. В противном случае решение будет неустойчивым. Некорректно поставленные задачи решаются методами регуляризации. Суть их в том, что исходная, поставленная задача, путем введения так называемого параметра регуляризации заменяется другой, близкой (с точностью, зависящей от вводимого параметра регуляризации) к исходной, но корректно поставленной. Например, задача суммирования бесконечных степенных рядов не имеет решения. Ограничивая число слагаемых ряда, вводя тем самым параметр регуляризации (количество слагаемых), можно получить решение регуляризированной задачи, естественно приближенное. Другой пример: изменяя элементы матрицы системы линейно зависимых уравнений, стоящих на главной диагонали, на некоторую малую величину (параметр регуляризации), можно обеспечить не равное нулю значение определителя и найти единственное, хотя и приближенное решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.