Округление чисел. Прямые методы решения систем линейных алгебраических уравнений. Нормы векторов и матриц

Договоримся использовать в качестве аппроксимирующих функций φ(х) только многочлены или функции, составленные из многочленов, т.к они являются линейными функциями своих параметров и их вычисление сводится к выполнению конечного числа простейших арифметических операций сложения и умножения.

Будем считать, что аппроксимация f(х) производится с помощью многочленов степени n. Тогда, в зависимости от критерия согласия и, в частности, от количества точек согласования f(x) и φ(х) (будем называть их узлами), можно рассмотреть разные конкретные способы аппроксимации.

9. Интерполяционный многочлен Лагранжа.

Пусть в точках , таких, что  известны значения функции f(x)=y , т.е. на отрезке [a,b] задана табличная функция f(x):                                                                                    

Функция φ(х) называется интерполирующей или интерполяционной для f(x) на [a,b], если ее значения  в заданных точках , называемых узлами интерполяции, совпадают с заданными значениями функции f(x), т.е. с .

Геометрически факт интерполирования означает, что график функции φ(х) проходит так, что, по меньшей мере, в (n+1) заданных точках он пересекает или касается графика f(x).

Легко представить, что таких графиков φ(х), проходящих через заданные точки, можно изобразить сколько угодно, и они могут отличаться от графика f(x) сколь угодно сильно, если не накладывать на f(x) и φ(х) определенных ограничений.

Тогда задача интерполяции формулируется так:

для функции f(x), заданной таблицей (2), найти многочлен  такой, что выполняется совокупность условий интерполяции       .                                (3)    

Найти многочлен   - это значит, учитывая его каноническую форму    , найти его  n+1 коэффициент                                   (4)  

Для этого имеется как раз  n+1   условие  (3).

Таким образом, чтобы многочлен (4) был интерполяционным для функции (2), нужно чтобы его коэффициенты     удовлетворяли системе уравнений:

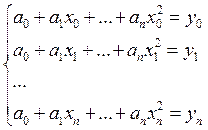
Базисные многочлены Лагранжа имеют вид 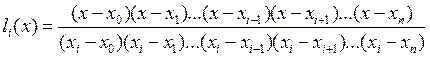, а искомый интерполяционный многочлен Лагранжа есть 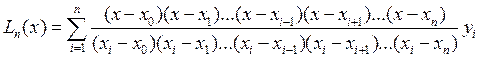         (6)

    Заметим, что числитель дроби, фигурирующий в записи i –го слагаемого  , представляет собой произведение разностей между переменной x и всеми узлами, кроме  i –го, а знаменатель – произведение разностей между i –м узлом и всеми остальными.

В качестве примера запишем интерполяционные многочлены Лагранжа первой и второй степени.

При n=1 информация об интерполируемой функции сосредоточена в двух точках  и . Многочлен Лагранжа в этом случае составляется с помощью двух базисных многочленов первой степени ( и ) и имеет вид 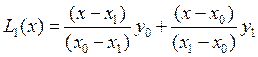   (7)

При n=2 по трехточечной таблице 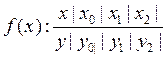 можно обрабатывать три базисных многочлена (, и ) и соответственно итерационный многочлен Лагранжа второй степени имеет вид

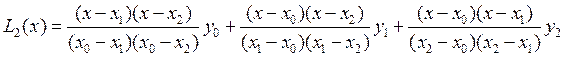                                   (8)

Приближенные равенства   и   называются соответственно формулами линейной и квадратичной интерполяции. Геометрически они означают подмену графика функции   на некотором отрезке [а,b]  оси абсцисс, содержащем точки  в первом и  во втором случаях, соответственно участками прямой линии и квадратной параболы, проходящих через заданные точки координатной плоскости.

Пусть для заданной функции  интерполяционный многочлен  построен, т.е. для приближенного представления   на отрезке [а,b]  [] применена интерполяционная формула                  (9).

Поиск погрешности.

Будем выяснять величину отклонения от в произвольной точке [а,b], иначе, величину остаточного члена        интерполяционной формулы (9)  в предположении, что  , т.е. данная функция  n+1 раз непрерывно дифференцируема. Если известна величина    , то оценить абсолютную погрешность интерполяционной формулы  (9)  в точке  можно с помощью неравенства:  .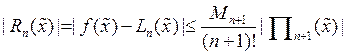                                  

Максимальная погрешность интерполирования на   оценивается величиной