Основи кореляційно-регресійного аналізу: Методичні вказівки для вивчення теми курсів “Теорія ймовірностей та математична статистика”, “Економетріка” і “Математика для економістів”, страница 6

Таблиця 5

Дисперсійний аналіз (I)
для перевірки значущості кореляційного зв'язку

Загальна мінливість (дисперсія) і число ступенів cвободи мають такий самий розклад, як і для результативної ознаки:

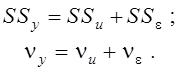
В другій графі таблиці дисперсійного аналізу записуються так звані “суми квадратів” (SS – Sum of Squares) відхилень:

 .

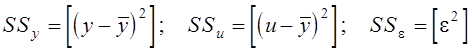Раніш вже були обчислені значення оцінок дисперсій  ,  звідки:

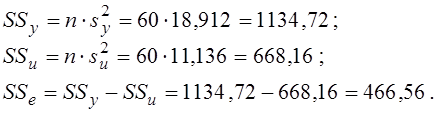
Числа ступенів свободи (ЧСС) у закордонній літературі позначаються як MF (Measure of Freedom)  або  d.f. (degree of freedom). Число ступенів свободи дорівнює числу випадкових величин мінус число лінійних зв’язків, накладених на ці величини. Оскільки на відхилення даних від загального середнього накладено один зв’язок (сума цих відхилень за всіма спостереженнями дорівнює нулю ), то загальне число ступенів свободи  дорівнюватиме:

n_y  = n ‑ 1 = 60 ‑ 1 = 59 .

На випадкові похибки e _ij накладені  k  зв’язків (тому що в кожній групі суми цих похибок дорівнюють нулю), звідки

n_e  = n ‑ k = 60 ‑ 6 = 54 .

Останнє число ступенів свободи одержимо як різницю:

n_u = n_y ‑ n_e = k  ‑ 1 = 6 ‑ 1 = 5 .

Середні квадрати MS (mean of square) часто позначають ; вони являють собою так звані “незсунені оцінки дисперсії”:

 .

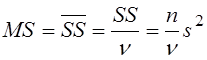Дисперсія – це середній квадрат відхилень від центру угрупування сукупності (від математичного очікування), а. вибіркова дисперсія – це середній квадрат відхилень від вибіркового середнього; тому вибіркова оцінка дисперсії, як правило, виявляється заниженою (зсуненою). Коефіцієнт  ⁿ /_n  призначений для виправлення зсуву і зветься “поправкою на незсуненість”.

У закордонній літературі використовуються тільки незсунені оцінки дисперсії і позначення  s²  закріплене саме за цім поняттям. Треба це мати на увазі. Корисно порівняти значення зсунених і незсунених оцінок дисперсії ( – для загальної дисперсії різниця ще невелика; але  – тут поправка на незсуненість виявилася більше 10).

Дисперсійне відношення Фішера – є відношення незсунених оцінок дисперсії 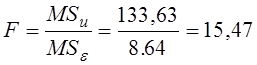; воно показує, у скільки разів мінливість “корисного сигналу” перевищує мінливість “шуму”. За табл. 5 одержано, що мінливість “корисного сигналу” (u) більше, ніж у 15 разів перевищує мінливість “шуму” (e).

В останніх двох графах таблиці виписані граничні значення критерію Фішера. Нижня межа F_0,05(5, 54)=2,47 показує, що при відсутності будь-якого “корисного сигналу” значення F можуть досягати цієї межі (якщо F<F_0,05 , “нуль-гіпотеза” не може бути відхилена). Друга межа F_0,01(5, 4)=3,34 дуже рідко досягається випадково (за відсутності “корисного сигналу”). Якщо F>F_0,01 , то більш розумно припустити, що такі великі відхилення невипадкові, вони викликані наявністю якогось ефекту (наявністю значущого “корисного сигналу”). У даному прикладі F=15,47 майже в 5 разів перевищує межу F_0,01=3,34 , тому “нуль-гіпотеза” про відсутність кореляційного зв’язку відхиляється, отже, у даному прикладі має місце значуща кореляційна залежність.

Замість останніх двох граф, що містять табличні значення F_0,05 і F_0,01 , іноді в таблиці присутня графа “Рівень значущості” (Signum of level), у якій наводиться ймовірність (a) того, що значення F, що спостерігається, отримано випадково при справедливості нуль-гіпотези. Це значення a  треба порівнювати із стандартними межами  0,05 і 0,01. Якщо a > 0,05, то “нуль-гіпотеза” не може бути відхилена; навпаки, якщо a < 0,01 – “нуль-гіпотеза” відхиляється.