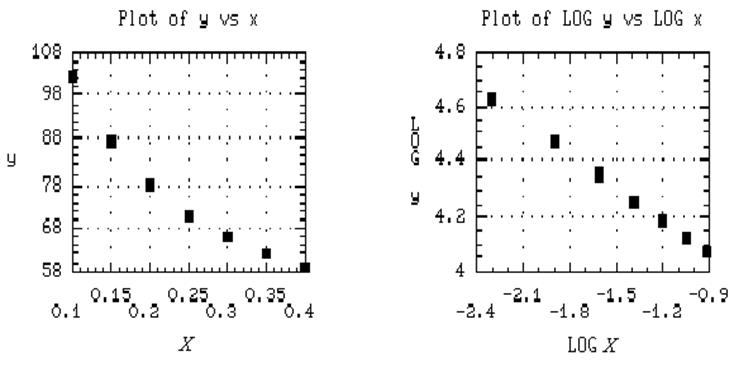
У функціональних логарифмічних координатах X=log(x), Y=log(y) степеневі залежності при будь-яких значеннях параметрів є лінійними. На рис. 12 б показано розташування емпіричних точок в перетворених координатах, звідки видно, що в логарифмічних масштабах точки добре укладаються на деяку пряму, тому гіпотеза про степеневу форму зв’язку тут “не може бути відхилена”.
а б
Рис. 12. Розташування вихідних точок у вихідних (à)
і логарифмічних (б) координатах
Графік степеневої залежності при значеннях параметра 0<b<1 має такі характерні риси – обидві вісі координат є асимптотами. Але ці особливості даної форми зв’язку не суперечать фізичним уявленням про процес. Дійсно, при дуже великій швидкості подачі (x®¥) швидкість різання спадає до нуля (y®0), а при дуже малій швидкості подачі (x®0) швидкість різання може бути як завгодно великою (y®¥). Ці міркування зміцнюють нашу впевненість у правильності вибору степеневої форми зв’язку.
Найчастіше застосовується або логарифмування змінних, або перехід до зворотних величин. У табл. 9 наведені довідкові відомості про нелінійні залежності, що можуть бути зведені до лінійних зазначеними функціональними перетвореннями. Для ілюстрацій у табл. 9 обрані тільки зростаючі залежності (по можливості регресивні). Розглядаючи цю таблицю переконуємося, що серед двопараметричних моделей відсутні форми зв’язку з екстремумами (з максимумом, або з мінімумом). Це дуже серйозне обмеження. Фахівець - прикладник вірить, що якщо його дані оброблені на комп’ютері, то знайдена модель дозволить йому згодом визначити оптимальні значення параметрів для одержання максимального ефекту. На жаль, це не зовсім так. Аналіз даних являє собою маленьке наукове дослідження і не може бути проведеним конвеєрним способом малокваліфікованим персоналом. Звичайно при стандартному розрахунку, як правило, розглядається лише лінійна модель, або одна з розглянутих вище двопараметричних залежностей. Але тоді подальший аналіз покаже відсутність оптимумів, причому не тому, що їх немає в дійсності, а тому, що обрана форма зв’язку не припускає їхньої наявності у принципі ні при яких значеннях параметрів.
Таблиця 9.
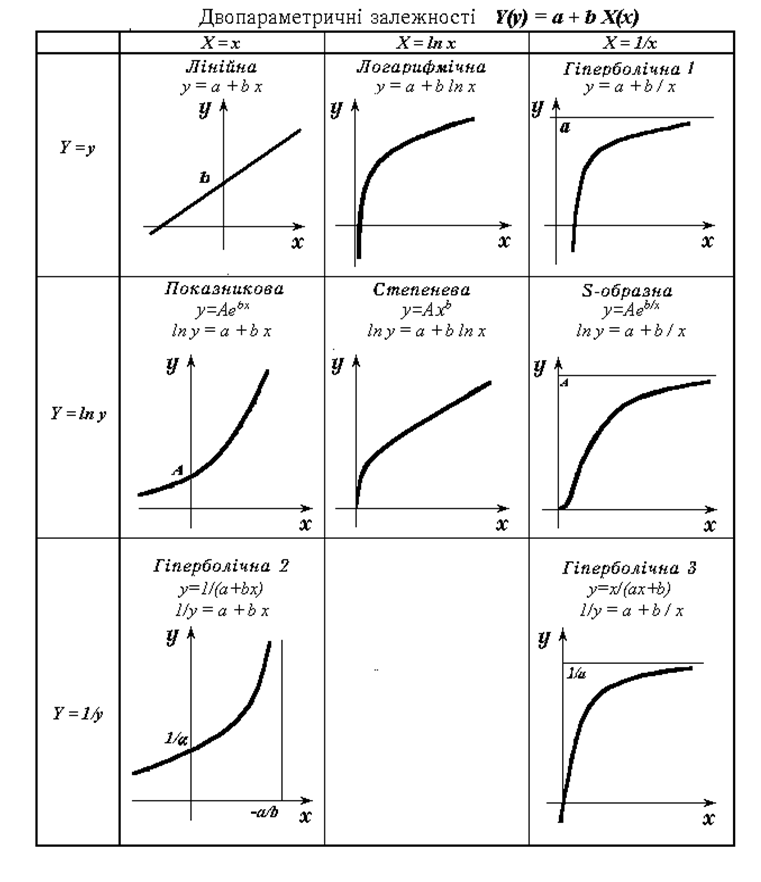
Якщо ми припускаємо наявність оптимумів, то варто використовувати трьохпараметричні форми зв’язку, наприклад, квадратичну модель. Квадратична модель повинна бути прийнята як базова при аналізі даних, хоча вона значно складніша за лінійну (особливо в багатомірному випадку).
Узагальнена квадратична модель з функціональними перетвореннями змінних здатна адекватно описати дуже широкий клас залежностей з екстремумами.
За допомогою функціональних перетворень змінних можна знайти форму зв’язку, яка найкращим чином відповідає емпіричним даним. Але слід пам’ятати, що при функціональних перетвореннях результативної ознаки змінюється вся система похибок e і це може призвести до небажаних наслідків. Як відомо, одне з головних передумов регресійного аналізу вимагає рівноточності спостережень, тобто похибки для будь–яких значень аргументів х повинні мати однакову дисперсію (ця властивість зветься “гомоскедастичністю”, протилежна властивість зветься “гетероскедастичністю”). Саме гомоскедастичність порушується при функціональних перетвореннях результативної ознаки у.
Дійсно, нехай наша нелінійна модель
y = yp(b, x) + e
після функціонального перетворення F(y) зводиться до лінійної моделі щодо параметрів:
F(y‑ e) = F(yp(b, x)) = b0 X0 + b1 X1 .
Розкладемо F(y‑ e) у ряд Тейлора–Маклорена по ступенях малих похибок e і обмежимося першими двома членами:
F(y‑ e) = F(y) – e F'(y) = Y ‑ e ,
де позначено Y = F(y) ; e = e F'(y) .
Тоді формально одержуємо лінійну модель
Y = b0 X0 + b1 X1 + e ,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.