Случайный процесс. Случайный поток событий. Простейший поток событий. Суперпозиция нескольких простейших потоков. Прореживание простейшего потока, страница 3

P(x_S³x)=P({x₁³x}Ç{x₂³x})=P(x₁³x)*P(x₂³x)=[1–P(x₁<x)]*[1–P(x₂<x)]=

=[1–F_x1(x)]*[1–F_x2(x)]=[1–1+exp(–l₁×x)]* [1–1+exp(–l₂×x)]=exp(–l₁×x)*exp(–l₂×x)=

=exp(–(l₁+l₂)×x).

Следовательно, F_xS(x)=P(x_S<x)=1–P(x_S³x)=1–exp(–(l₁+l₂)×x), таким образом, время между событиями результирующего потока событий имеет показательный закон распределения с параметром ((l₁+l₂)).

Вывод. Поток событий, образованный суперпозицией двух простейших потоков событий с параметрами l₁ и l₂ , является простейшим потоком событий с параметром (l₁+l₂).

Теорема (о суперпозиции n независимых простейших потоков). Поток событий, образованный суперпозицией n независимых простейших потоков событий с параметрами l₁ , l₂ ,…l_n , является простейшим потоком событий с параметром l_S=l₁+l₂+…+l_n . Следовательно, время между событиями результирующего потока событий имеет показательный закон распределения с математическим ожиданием M[x_S]=1/l_S=1/(l₁+l₂+…+l_n.).

Теорема (о законе распределения минимальной из n независимых случайных величин) (без доказательства). Закон распределения случайной величины, равной минимальному значению из n независимых случайных величин, принимающих лишь положительные значения, в пределе n®¥ стремится к показательному распределению. Т.е. если x=min{x₁ , x₂ ,…x_n }, где x_i>0 " i=1,…n, то .

Теорема (о суперпозиции бесконечного числа независимых потоков событий) (следствие предыдущей теоремы). Поток событий, образованный суперпозицией бесконечного числа независимых потоков событий (не обязательно простейших), является простейшим потоком событий с параметром l_S=(M^–1[x₁]+M^–1[x₂]+…+ M^–1[x_n]+...), где M[x_n] – среднее время между событиями n-го потока событий.

Практическая значимость указанных теорем состоит, например, в том, что в теории надёжности интенсивности отказов системы, который складывается из потоков отказов компонентов системы, с увеличением числа компонентов приближается к простейшему потоку (следовательно, характеризуется только математическим ожиданием времени наработки системы на отказ), даже если потоки отказов компонентов не являются простейшими.

Случайное и регулярное прореживание простейшего потока событий

Часто встречается ситуация, когда не все события потока проходят через некоторое разрешающее устройство. Например, не каждый посетитель магазина делает покупки, т.е. является посетителем кассы. Другой пример: не все отказы систем железнодорожной автоматики и телемеханики являются опасными. Некоторые из них являются защитными и могут быть вовремя устранены электромонтёром.

Таким образом, лишь некоторые события исходного потока образуют результирующий поток событий. Если сквозь «решающее устройство» проходит строго каждое k-ое событие исходного потока, то такое прореживание потока событий называется регулярным. Если же каждое из событий исходного потока проходит через «решающее устройство» с вероятностью Pо, и, соответственно, «задерживается» в нём с вероятностью (1–Pо), то такое прореживание называется случайным.

Часто встаёт задача определения характеристик результирующего потока событий исходя из характеристик исходного потока и свойств прореживающего устройства.

Теорема (о случайном прореживании простейшего потока событий) (без доказательства). Поток событий, образованный случайным прореживанием простейшего потока событий с параметром l₁ с вероятностью Pо, также является простейшим потоком событий с интенсивностью l₂=l₁Pо (т.е. меньшей интенсивностью).

Следовательно, время между событиями потока событий, образованного случайным прореживанием простейшего потока, имеет показательный закон распределения со средним значением (l₁Pо)^–1.

Теорема (о регулярном прореживании простейшего потока событий) (без доказательства). Время x₂ между событиями потока, образованного регулярным прореживанием простейшего потока событий с параметром l₁, когда пропускалось лишь каждое k-ое событие исходного потока (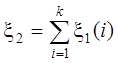), имеет закон распределения Эрланга k-го порядка с параметром l₁.

Практическая значимость предлагаемых теорем состоит в том, что, зная характеристики потока посетителей магазина, можно прогнозировать время, через которое будут поступать посетители в кассу магазина. Или же можно определить показатели потока опасных отказов систем на основе информации об общем потоке отказов системы. Вероятность того, что некоторый отказ системы является опасным можно определить анализом структуры системы.