Последовательности независимых событий и величин. Неравенство Чебышева. Типы сходимости

IV.  Предельные теоремы теории вероятностей

4.1  Последовательности независимых событий

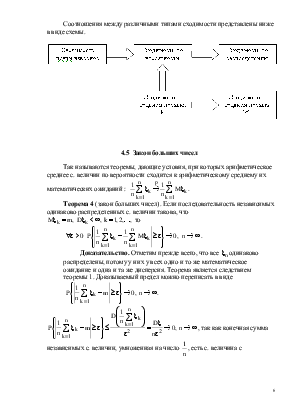
Рассмотрим некоторое вероятностное пространство (Ω, F, P). Будем говорить, что события  независимы, если для всех m, , и  всех   .

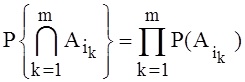Будем говорить, что события   образуют последовательность независимых событий, если для любых nсобытия  независимы.

Если  - последовательность независимых событий, то последовательность где или , также последовательность независимых событий.

С каждой последовательностью событий можно связать события

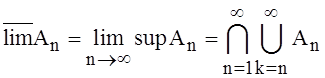
и                                                                                             (4.1)

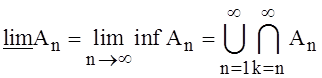
Первое из событий (4.1) означает, что для любого nосуществляется хотя бы одно из событий , k = n, n+1,… т.е. событие осуществляется тогда и только тогда, когда происходит бесконечное число из событий .

Второе из событий (4.1) означает, что существует такое число n, что осуществляются все события ,  k = n, n+1,…  т.е. событие происходит тогда и только тогда, когда не происходит лишь конечное число из событий .

Теорема 1 (Бореля - Кантелли). Если  - последовательность независимых событий, то:

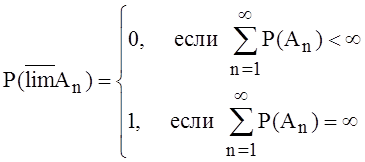
Доказательство. В первом случае из соотношения

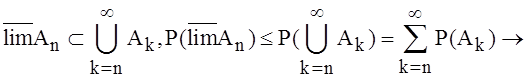 0  при  

как остаток сходящегося ряда. Во втором случае перейдем к событию

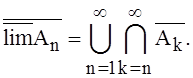
Тогда

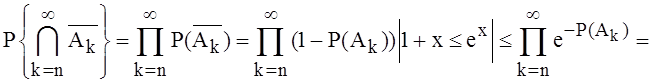
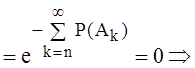
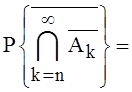
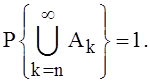
Так как 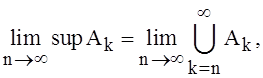   то  в этом случае.

В чем смысл доказанной теоремы? Для независимых событий событие может иметь вероятность 0 или 1. В первом случае это означает что с вероятностью 1 происходит лишь конечное число из событий ; во втором – с вероятностью 1 происходит бесконечное множество событий из .

4.2  Последовательности  независимых величин

Пусть  - последовательность независимых с. величин. Это значит, что  и любых чисел события  независимы.

Замечание. Следует помнить, что когда мы говорим пусть x – с. величина или пусть – последовательность  с. величин, то полагаем, что существует некоторое вероятностное пространство (W, F, P), на котором эта с. величина x  или эти с. величины  заданы.

Приведем некоторые признаки независимости с. величин.

Теорема 2.  Для того, чтобы с. величины  были независимы необходимо, чтобы для любых ограниченных борелевских функций    

=    (4.2)

и достаточно, чтобы равенство (4.2) выполнялось для непрерывных ограниченных функций.

Борелевскими называются функции, измеримые относительно s– алгебры борелевских множеств.

Следствие 1. Если  - независимые с. величины и , существуют, то существует и .

Следствие 2.  1). Если  -  независимые с. величины и , то  - не коррелированы;

2). Если   - независимые с. величины и  то

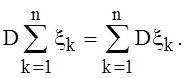
Результаты следствия 2 нам уже известны.

4.3   Неравенство Чебышева

Теорема 3.  Пусть x– неотрицательная с. величина с вероятностью 1 и существует . Тогда:

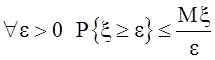                                                             (4.3).

Доказательство.  Введем в рассмотрение событие . Для него индикаторная функция имеет вид:

.  .

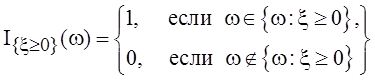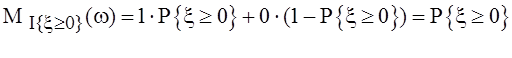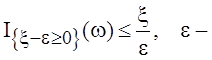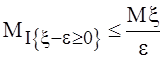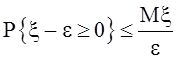Рассмотрим теперь очевидное неравенство  любое положительное число. Тогда   или    или  .

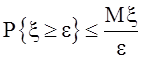Доказанное неравенство известно под названием неравенства Чебышева (правда иногда в литературе оно встречается под названием неравенство Маркова – [5] ).

Следствие.  Для произвольной с.величины x, имеющей дисперсию Dx,

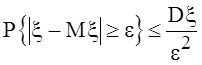                                                              (4.4)

Именно это неравенство известно широкому кругу читателей под названием неравенства Чебышева. Оно получается из теоремы 3, если в качестве с. величины  взять

Неравенство  эквивалентно неравенству . Поэтому  .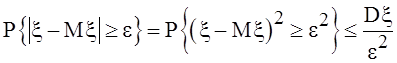

Однако,  оно может быть доказано и без помощи теоремы 3.  Введем в рассмотрение с.величину  .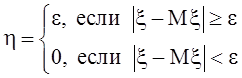

Тогда  

Но  Следовательно,  и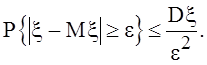

Неравенство (4.4) следует применять, когда , иначе оно дает тривиальную оценку.

Пример 1.  Пусть с величина xимеет плотность распределения 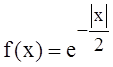. Тогда Mx=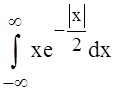=0 (интеграл от нечетной функции по симметричному множеству),

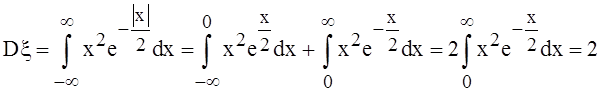
(интегрировали по частям).

Оценим при e=2,5,10. Получим

. Прямое  вычисление величин дает выражения

 .

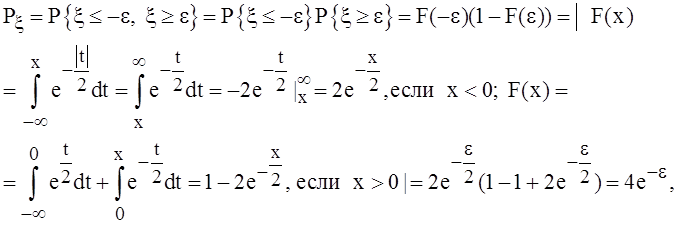
Видим, что неравенство Чебышева дает довольно грубые оценки вероятностей. Однако неравенство Чебышева является родоначальником многих других неравенств, широко применяемых в теории вероятностей.

4.4  Типы сходимости

Пусть дана некоторая последовательность с. величин  и с. величина x.  

Определение 1.   Говорят, что последовательность с. величин сходится к с. величине xпочти наверное (с вероятностью 1), если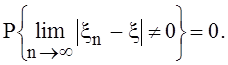

Иными словами говоря, равенство 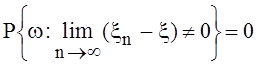 означает, что множество тех w, для которых последовательность  имеет вероятностную меру 0.

Обозначение: 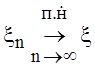  или

Определение 2.   Говорят, что последовательность с. величин сходится к с. величине xпо вероятности, если 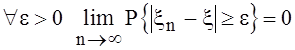. Обозначение:

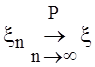  или

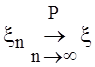Эти два вида сходимости связаны между собой: из сходимости почти наверное следует сходимость по вероятности. Обратное утверждение не имеет места, но если последовательность  , то любая её подпоследовательность содержит другую подпоследовательность, сходящуюся по вероятности 1 [3].

Определение 3.  Говорят, что последовательность с. величин сходится к с. величине xв среднем порядка p, если .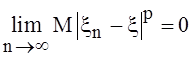

В анализе этот вид сходимости  называют сходимостью в смысле . Поэтому обозначают этот вид сходимости так: .

При p = 2 сходимость называют сходимостью в среднем квадратичном (среднем квадратическом), обозначают это так:  (от limit in the mean) или  .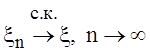

Определение 4.  Пусть с. величины имеют функции распределения , а с. величина x - F(x). Говорят, что последовательность с. величин сходится по распределению к с. величине x, если  во всех точках непрерывности функции F. Обозначение: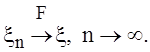

Говорят ещё в этом случае, что последовательность функций распределения  слабо сходится к функции распределения .