Выше было рассмотрено получение плотности распределения f(x) по известной функции распределения, как ее первая производная:
f(x)=F’(x)
На практике чаще возникает обратная задача:
Дано: f(x)
Определить: F(x)
В этом случае функция распределения F(x) равна:
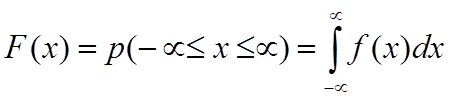
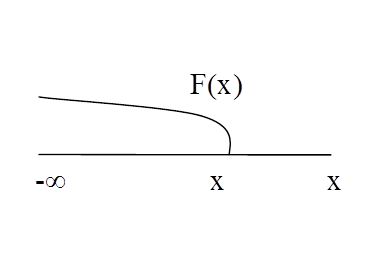 F(x)=p(X<x)
F(x)=p(X<x)
16 Числовые характеристики СВ. Общие соображения
В реальной действительности любые СВ как ДСВ так и НСВ могут быть охарактеризованы некоторыми числовыми характеристиками, которые являются некоторым эквивалентом их законов распределения.
Различают два класса числовых характеристик:
1) Характеризуют некоторый центр рассеяния – среднее значение СВ. Относительно этого центра (среднего) СВ группируются, хотя они одновременно и рассеиваются. Свойство некоторого среднего таково что его положение отражает флуктуации (относительное отклонение) СВ относительно среднего значения.
Характеристиками среднего является – математическое ожидание, мода, медиана.
2) Характеризует саму величину рассеяния относительно среднего значения СВ Х. Так, например, при одном и том же среднем рассеивании относительно него может быть различно и чем оно больше, тем выше неопределенность. Числовыми характеристиками рассеивания являются – дисперсия и среднеквадратическое отклонение.
3.8 Математическое ожидание СВ
Термин математическое ожидание (МО) – возник со времен азартных игр и подразумевал собой ожидание выигрыша. С утверждением теории вероятности возник уточненный термин МО СВ, который в дальнейшем в серьезных дисциплинах избавился от слова выигрыш. Это обусловлено тем, что МО может быть найдено для любого параметра.
![]() – математическое ожидание, где М – оператор
взятия МО
– математическое ожидание, где М – оператор
взятия МО
Для конкретных параметров:
1) Напряжение
![]()
Пусть на некоторой числовой оси имеется некоторое число значений СВ Х с соответствующими им СВ:
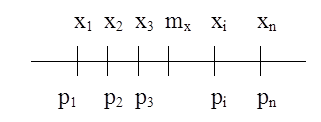 x1, x2, x3,…, xi,…,
xn
x1, x2, x3,…, xi,…,
xn
p1, p2, p3,…, pi,…, pn
Графически на числовой оси:
МО ДСВ есть сумма произведений всех возможных значений СВ на вероятности этих значений:
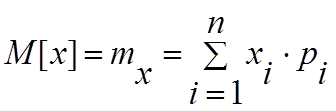
С физической точки зрения МО представляет собой некоторое среднеквадратичное значение (среднее), которому в механике соответствует центр тяжести.
В нашем случае значения СВ хi представляют собой некоторое плечо, а соответствующие им вероятности рi – некоторый вес. Иначе говоря, каждая величина входит в МО со своим весом. Этим МО отличается от среднего арифметического.
Таким образом, МО строго говоря является не просто средним, а среднестатистическим (средневзвешенным).
МО по своему физическому смыслу соответствует точке опоры, в которой техническая система находится в состоянии равновесия, состоянии устойчивости.
Т.к. вероятности в общие случае определяются статистически: рi*=mi/n, где рi* – статистический вес, n – вес опоры.
Доказано:
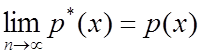
В связи с этим в соответствии с теоремой Чебышева во многих случаях ищется среднее арифметическое и находится его ошибка. Для НСВ МО:
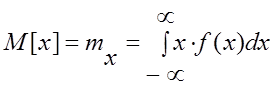 , где f(x)dx=pi (см. предыдущую лекцию).
, где f(x)dx=pi (см. предыдущую лекцию).
Таким образом, МО является важным понятием в теории вероятности, которое позволяет дать устойчивые статистические оценки некоторого среднего значения от Х, относительно которого флуктуирует (колеблется) СВ. В частном случае, если СВ распределена на интервале [a;b], то очевидно:
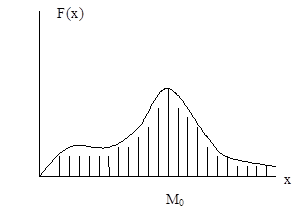
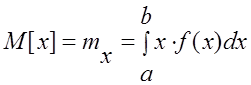
2)Mode – характеризует некоторое среднее значение, для которого вероятность максимальна.
М0=maxp(x)
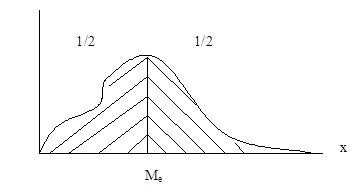
3) Mediana – значение СВ , для которого вероятность попадания СВ слева и справа одинакова и равна ½.
Me=p(x<Me)=p(x>Me)=1/2
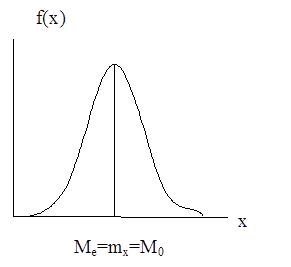
Для унимодальных законов (одновершинных и симметричных) все три характеристики совпадают.
3.9 Свойства математического ожидания
1) M[c]=c, где c=const
Доказательство:
M[c]=c*p=c*1=c
2) МО нуля равно нулю (вытекает из предыдущего)
3) M[c*x]=c*M[x]
4) МО произведения двух независимых СВ равно произведению их МО.
M[x*y]=M[x]*M[y]
5) МО суммы или разности двух СВ равно МО их суммы или разности.
M[x±y]=M[x] ±M[y]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.