Вероятностное пространство. Пространство элементарных событий. Определение вероятностного пространства

1  ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО

1.1   Пространство элементарных событий

       Для построения математической модели случайных событий может быть выбрано произвольное непустое множество , называемое в теории вероятностей пространством элементарных событий.  Элементы этого множества называются элементарными событиями.

      При вероятностном моделировании случайных событий выбор множества  зависит от конкретных условий.

      Пример 1.При однократном бросании игральной кости может выпасть 1, 2, …, 6 очков. Если в задаче обсуждаются возможности выпадения на верхней грани того или иного числа, тогда в качестве пространства элементарных событий естественно выбрать конечное множество .

      Однако при одинаковых начальных условиях в зависимости от  задачи выбор пространства элементарных событий может быть не однозначным.

       Пример 2.  При таких же условиях, как в примере 1, нас может интересовать только факт выпадения четного или нечетного числа. Здесь в качестве пространства элементарных событий следует выбрать множества из двух элементов: .

      Пример 3. В результате каждого экзамена присутствует элемент случайности. Студент, явившийся сдавать экзамен, обязательно получит один из четырех баллов. Здесь пространство элементарных событий   Однако и здесь при выборе пространства элементарных событий может возникнуть неоднозначность. Пусть, например, интересен только один результат: сдал экзамен или не сдал. Тогда эти два возможных результата и образуют пространство элементарных событий:

     Как мы уже было сказано,  пространство элементарных событий может представлять произвольное непустое множество: конечное или бесконечное, счетное или непрерывное – все зависит от смысла поставленной задачи.

1.2  Алгебра событий

      Над пространством элементарных событий строится новое множество . Элементами этого множества являются все возможные подмножества :

 а также в него в качестве элементов включаются пустое множество  и само исходное множество :

,  .

                    На множестве  определены операции отрицания , объединения  и пересечения , в результате которых получаются также элементы множества  и при этом справедливы следующие свойства операций:

1.,   ;

2.,   ;

3.,

    ;

4.,

   ;

5.,   ;

6.,   ;

7.,    ;

8.  ,   ;

9.,   ;

10.,   .

       Предположим также, что результат операций объединения и пересечения  для бесконечной последовательности  элементов этого множества   А₁, А ₂, . . . , А_n, . . .  Î   является элементом того же множества . Это последнее коротко запишем так:

,        .

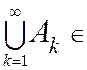
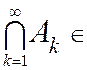
      Такое множество называется алгеброй событий, а его элементы  А, В, . . . – событиями, W  – достоверным событием,  Æ - невозможным событием. Если  A Ì B, то событие А называется частным случаем события В.

      Заметим, что в зависимости от контекста символы   W   и  Æ  имеют различное значение:  W – пространство  элементарных событий (произвольное непустое множество)  и   – достоверное событие,   Æ  – пустое множество  и    –  невозможное событие.

      Свойства алгебры событий позволяют производить операции над событиями по правилам операций над множествами. Операцию отрицания в этом случае выполняем как операцию  W \ А.

      Пример 4.  Примем в качестве пространства элементарных событий  числовое множество  W = [0, 1]. События  А  и  В  определены так:   A = [0; 0,5),  B= [2,5; 0,8).  Определить события  ,  ,       AÈB, AÇ B,  Ç ,  Ç В.

      Выполняя указанные операции, получаем

  = [0,5; 1],       = [0; 0,25) È [0,8; 1],

                           AÈ B= [0; 0,8),     AÇ B= [0,25; 0,5),

                           Ç  = [0,8; 1],    Ç В = [0,5; 0,8).

Пример 5.Убедиться в справедливости равенств:

1) =А; 2) =.

·  1) 

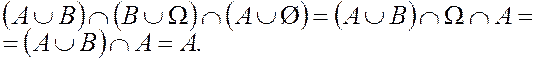
б)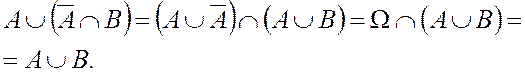    

Пример 6.  Событие  состоит в том, что произойдет событие  и хотя бы одно из трех событий . Выразить событие  с помощью операций алгебры событий через .

·  .

Это же событие    можно представить иначе:

 

1. 3  Определение  вероятностного пространства

Для пространства элементарных событий  и алгебры событий  определена числовая функция, которая каждому событию  ставит в соответствие некоторое число  и удовлетворяет следующим аксиомам:

1.   .

2.   .

3.   если ,  то  .

4.  если  и при этом 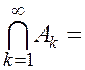, тогда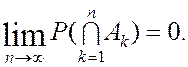

Функция  называется вероятностной мерой, а структура, определяемая пространством элементарных событий , алгеброй событий  и вероятностной мерой , называется вероятностным пространством и обозначается тройкой .

Значения функции  для конкретных событий  называются вероятностями этих событий и обозначаются , .

Основные следствия из аксиом:

 1.  ;

 2.  ;

 3.  ;

 4.  если , то .