Информатика и выч. техника \ Криптографические методы защиты информации

Исследование алгебраических и вероятностных свойств криптографических примитивов (Лабораторная работа № 4), страница 3

q  КСЛЭ, если разность Df(X, b) является сбалансированной функцией для любых a, вес которых  wt(a) =1;

q  КСЛЭ порядка k (SAC(k)), если любая функция, полученная из f(X) путем подстановки констант на места произвольных ее k переменных, удовлетворяет КСЛЭ.

Переходя к спектральным свойствам БФ f(X) удовлетворяет КСЛЭ, если АКФ rb(f )=0 для любых векторов bÎGF(2)n, вес которых wt(b)=1.

Булева функция f(X), XÎGF(2)n удовлетворяет:

q  КР степени l£n (PC(l)), если при замене 1 £ i £ l произвольных входных битов на свои дополнения функция f(X) изменяется с вероятностью Pr{f(X) ¹ f(XÅb)} = 0.5, что эквивалентно сбалансированности разности Df(X, b) для любых b, вес которых 1£  wt(b) £ l;

q  КР степени l £ n и порядка k £ n-1 (PC(l)/k ), если любая функция, полученная из БФ f(X) фиксацией любых ее k переменных, удовлетворяет PC(l).

В терминах спектральных свойств БФ удовлетворяет КР степени l (PC(l)), если ее АКФ rb(f ) = 0 на всех векторах bÎGF(2)n, вес Хэмминга которых лежит пределах 1 £ wt(b) £ l. Очевидно, что КР является обобщением КСЛЭ, точнее КСЛЭ эквивалентен КР PC(1).

Исследование нелинейности БФ

При анализе эффективности криптографических преобразований, в частности в отношении линейного криптоанализа, одной из основных характеристик является нелинейность БФ, реализующих данное преобразование, которая показывает степень удаленности БФ от множества аффинных или линейных БФ. Нелинейность БФ является важным показателем, поскольку линейные функции легко вскрываются криптоаналистическими методами.

Под аффинными функциями fафф(X)ÎA, где A = {fафф(X)}, XÎGF(2)n понимаются БФ следующего вида

fафф(X) = ,                                   (11)

где a, cÎGF(2). При c=0 аффинные функции образуют подмножество линейных функций L={fлин(X)}, каждая из которых является скалярным произведением  вида  fлин(X) = .

Удаленность БФ от множества аффинных A или линейных L БФ оценивается через расстояние Хемминга d(f, g) между двумя БФ f(X) и g(X), которое определяет количество отличающихся значений функций:

d(f, g) = #{f(X)¹g(X) : XÎGF(2)n} = wt(S(f )ÅS(g)).                          (12)

Данное расстояние можно определить через сопряженные функции

d(f, g) =  = 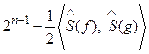.                        (13)

Коэффициент взаимной корреляции и расстояние Хемминга связаны между собой следующим соотношением:

r(f, g) = .                                                         (14)

Суммарная корреляция не зависит от вида функции f(X), и для любой БФ f(X) всегда существует корреляция с какой-либо линейной функцией, т. е. существует  такая fлинÎL, что .

На основании вышеизложенного, дадим определение нелинейности БФ f(X) : GF(2)n®GF(2), под которой понимается значение минимального расстояния Хэмминга между функцией f(X) и функциями fафф(X)ÎA:

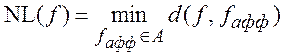.                             (15)

Аналогично нелинейность NL(f ) можно выразить через расстояние до линейных функций  в терминах ПУА:

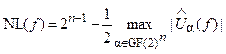,                            (16)

т.е. для определения нелинейности БФ следует определить максимальное значение компоненты спектра УА. Используя данное соотношение, можно достаточно просто определять нелинейность БФ при малых значениях n.

На основании теоремы Парсеваля верхняя граница значения нелинейности NL(f) для любых БФ f(X), X Î GF(2)n, определяется неравенством

NL(f) £ 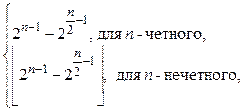                        (17)

где  означает максимальное четное целое, меньшее либо равное значению аргумента.

Достичь наилучших показателей нелинейности для векторной БФ сложно, поэтому на практике используется понятие средней нелинейности векторной БФ j(X), которые определяются из выражений:

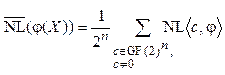.                                         (18)

Пределы нелинейности для векторных БФ j(X) совпадают с пределами для компонентных БФ.

Таким образом, обобщая изложенные результаты, сформулируем необходимые требования ко всему подстановочному преобразованию и к формирующим его компонентным БФ:

1.  Регулярность отображения Y=j(X) : GF(2)n®GF(2)m при n³m, т.е. сбалансированность всех компонентных БФ и их любых линейных комбинаций.

2.  Высокая алгебраическая степень нелинейности deg(f ) компонентных БФ.

3.  Соответствие БФ показателям корреляционной иммунности.

4.  Соответствие БФ КСЛЭ и КР из множества SAC(k), PC(k)/l, т.е. низкие автокорреляционные показатели.

5.  Высокая нелинейность NL(f ) компонентных БФ.

6.  Высокая нелинейность NL(j(X)) или средняя нелинейность  векторного преобразования.

Скачать файл