Получим систему нормальных уравнений
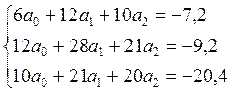
Решив систему, найдем а0 = -0,133; а1 = 2,086; а2 = -3,144. Таким образом, z = -0,133 + 2,086x – 3,144y.
Расчетные значения Zр и квадраты отклонений расчетных значений от фактических Zф приведены в табл. 11.
Табл. П11
|
X |
Y |
Zф |
Zр |
(Zф - Zр)2 |
|
1 |
1 |
-1,1 |
-1,191 |
0,008 |
|
2 |
1 |
0,9 |
0,895 |
0,000 |
|
3 |
3 |
-3,1 |
-3,307 |
0,043 |
|
1 |
2 |
-4,1 |
-4,335 |
0,055 |
|
2 |
2 |
-2,9 |
-2,249 |
0,424 |
|
3 |
3 |
3,1 |
2,981 |
0,014 |
|
Сумма |
0,544 |
|||
Для заданного уравнения регрессии z = a0 + a1x + a2y составим матрицу X и транспонированную матрицу XT
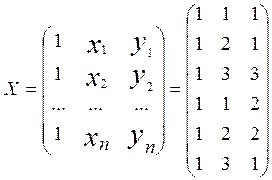
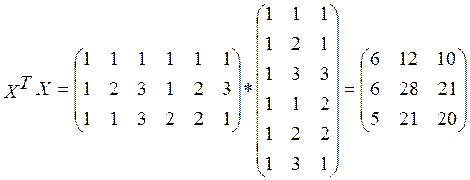
Матрица, обратная матрице системы нормальных уравнений, равна
.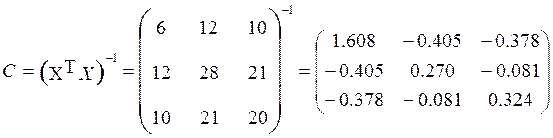
Для уровня значимости 0,05 и числа степеней свободы 6
– 3 = 3 по таблицам распределения Стьюдента находим t0,05 = 3,18. Тогда случайные ошибки для коэффициентов
регрессии, определяемые по формуле 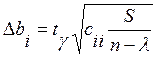 будут иметь следующие
значения:
будут иметь следующие
значения:
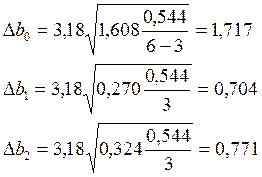
Таким образом, свободный член незначим при уровне
значимости 0,05(![]() ), а коэффициенты при x и y
значимы, т.е. можно считать, что уравнение регрессии имеет вид
), а коэффициенты при x и y
значимы, т.е. можно считать, что уравнение регрессии имеет вид
z = 2,086x – 3,144y.
Составим матрицу парных корреляций
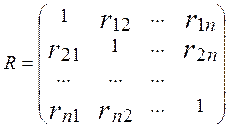
Парные коэффициенты регрессии можно найти с помощью матрицы С,
если каждый элемент этой
матрицы разделить на корень из произведения диагональных элементов, стоящих в
одной строке и водном столбце с этим элементом, т.е. 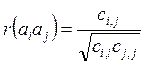
причем номера i и j должны точно соответствовать порядку номеров этих коэффициентов в уравнении регрессии и матрице-столбце А.
Преобразуем матрицу С в корреляционную матрицу по формуле (18.3) и получим
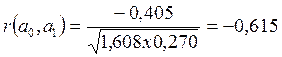
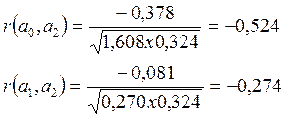
или 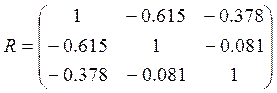
В
соответствии с критерием значимости коэффициентов корреляции 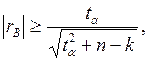
где n - объем выборки и k - число коэффициентов уравнения регрессии
имеем
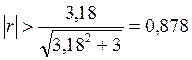
Таким образом, все коэффициенты корреляции между оценками коэффициентов регрессии незначимы и «эффекта смешивания» нет.
Оценим
частные коэффициенты корреляции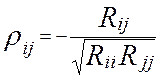 и множественные
коэффициенты корреляции.
и множественные
коэффициенты корреляции. 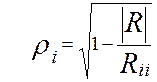
Где Rij - алгебраическое дополнение и │ R│- определитель матрицы оценок парных коэффициентов корреляции.
Разложим определитель матрицы R по первой строке (формула Лапласа).
![]()
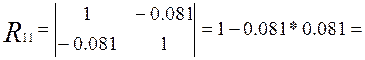
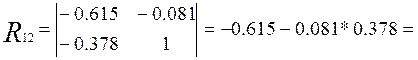
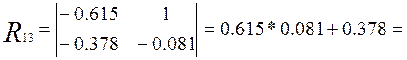
Критерии значимости коэффициентов корреляции.
1.Коэффициент корреляции rв, парный коэффициент корреляции rij и частный коэффициент корреляции ρij. (n - объем выборки). В случае частного коэффициента корреляции число степеней свободы рано ν=n-k, где n– объем выборки, k - число случайных величин в системе.
Проверяется нулевая гипотеза H0: r=0 (rij=0). По уровню значимости α и числу степеней свободы ν=n-2 по таблицам распределения Стьюдента находим критическое значение tα. Если выполняется неравенство
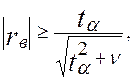
то гипотеза H0 отвергается, т.е. коэффициент корреляции не равен нулю. В этом случае говорят, что коэффициент корреляции значим при уровне значимости α.. Если же неравенство не выполняется, то нет оснований отвергнуть гипотезу H0, т. е. коэффициент корреляции незначим при уровне значимости α..
2. Множественный коэффициент корреляции.
Для проверки значимости множественного коэффициента корреляции (в частности коэффициента корреляции для системы двух величин, так как этот коэффициент корреляции является и парным, и множественным одновременно) определяется среднее квадратическое отклонение его оценки
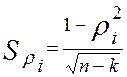
где n – объем выборки; k – число случайных величин в системе. По числу степеней свободы ν=n-k и уровню значимости α по таблицам Стьюдента находим tα . Критерий значимости определяется неравенством
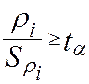
Отметим, что если по критерию () проверяется значимость коэффициента корреляции
для системы двух величин, то в числителе следует взять модуль его оценки.
Средние выборочные, исправленные выборочные дисперсии
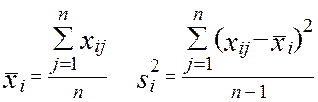
и оценки парных коэффициентов корреляции
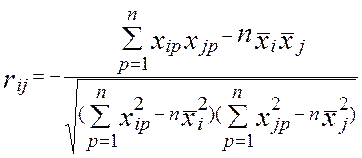
Матрица парных коэффициентов корреляции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.