







12. РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
МЕТОДОМ СЕТОК
12.1. Цель работы
Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Численные методы решения дифференциальных уравнений в частных производных», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.
12.2. Задание.
Найти приближенное решение уравнения Лапласа в заданной области с указанными граничными условиями, принять h1=h2=0.1
|
1. |
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
12.3 Теоретические сведения
Уравнение относительно неизвестной функции u(x,y) двух или более независимых переменных , которое содержит частные производные этой функции, называется уравнением в частных производных (УЧП).
В общем виде ДУ второго порядка относительно функции двух независимых переменных u(x,y) записывается так :
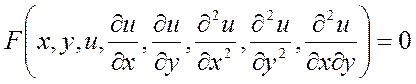 (12.1)
(12.1)
Функция F- заданная функция восьми аргументов .
Далее будем рассматривать линейные уравнения второго порядка :
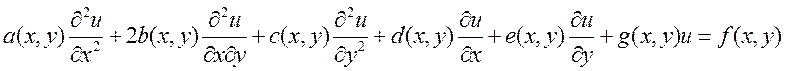 Все
коэффициенты и правая часть не зависят от u(x,y).
Все
коэффициенты и правая часть не зависят от u(x,y).
Методы классификации УЧП :
· По порядку уравнения ( наивысший порядок частных производных, входящих в уравнение)
· По числу переменных ( по числу независимых переменных )
· По критерию « линейное-нелинейное»
![]()
A,B,C,D,E,F,G – константы или заданные функции переменных x,y.
· По критерию «однородное-неоднородное»
Однородное , если G(x,y)≡0 для всех x и y.
Если G(x,y)≠0 – неоднородное .
· По виду коэффициентов
A,B,C,D,E,F,G – константы – уравнение с постоянными коэффициентами.
Основные типы УЧП :
· Параболический тип :
Описывает процессы теплопроводности и диффузии : B2=4AC
· Гиперболический тип
Описывает колебательные системы и волновые движения : B2>4AC
· Эллиптический тип
Описывает установившиеся процессы : B2<4AC
Введем понятие оператора первого и второго порядка :
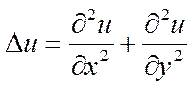
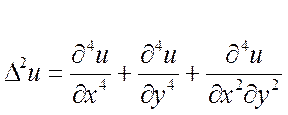
Решить задачу Дирихле для уравнения Лапласа значит найти приближенное решение уравнения в области D с граничными условиями:
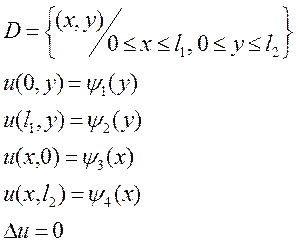 (12.2)
(12.2)
Искомая функция u(x,y) геометрически представляет собой некую поверхность с границами , заданными в виде функций ψ, которые проецируются на прямые стороны области D. Внутри поверхности и соответственно внутри прямоугольника значения u(x.y) неизвестны .
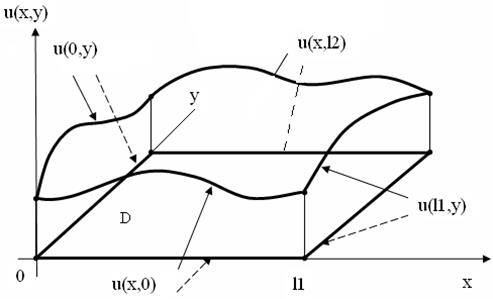
Рис.12.1
Сплошными линиями показаны граничные функции в пространстве, пунктиром - их проекции на стороны области D . Пусть l1=l2
Введем в рассмотрение узловые значения аргументов x и y с шагом h , тем самым переходя к дискретному аналогу непрерывной задачи.
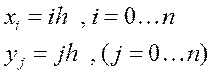 (12.3)
(12.3)
Тогда ![]() (12.4)
(12.4)
В каждом узле заменяем частные производные второго порядка разностными соотношениями :
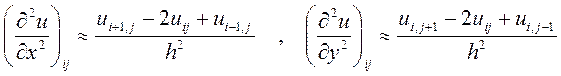 (12.5)
(12.5)
Выполненные замены позволяют свести решение уравнений с частными производными к решению системы разностных уравнений.
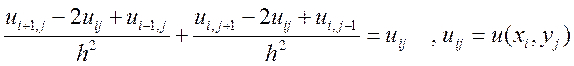 (12.6)
(12.6)
Уравнение (12.6) вместе со значениями uij в граничных узлах есть система линейных алгебраических уравнений относительно значений функции u=u(x,y) в узлах сетки. Погрешность замены ДУ составляет величину О(h2).
Для уравнения Лапласа система может быть записана в виде:
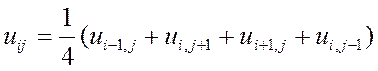
В данной работе система решается
методом простых итераций по формулам: 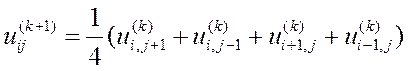
В качестве условия окончания
итерационного процесса можно принять: 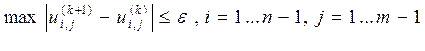
Данная разностная схема обладает свойством устойчивости и сходимости. Это означает , что выбрав достаточно малый шаг h можно сколь угодно точно численно решить исходную задачу.
12.4 Пример выполнения задания
Найти решение задачи Дирихле для уравнения Лапласа :
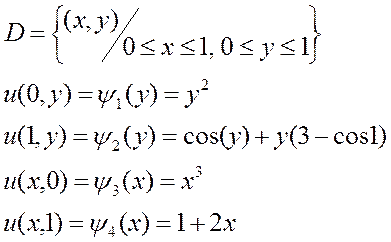
|
|
|
Нумерация элементов матриц начнется с 1 Краевые функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество узлов Краевые элементы матрицы искомой поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для начала расчета зададим начальное
приближение , то есть вектор ![]()
![]() в каждом слое. Рассмотрим слой с
точками (0,0.1) и (1,0.1).
в каждом слое. Рассмотрим слой с
точками (0,0.1) и (1,0.1).
u(1,0.1)
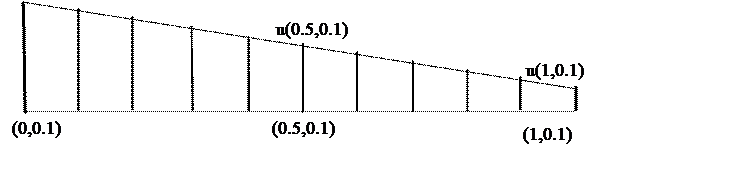
Рис. 12.1
Первоначально считаем, что изменение функции происходит равномерно , т.е. с некоторым постоянным шагом :
u1,2 = ψ1(0,0.1)=0.01 , u11,2 = ψ2(1,0.1)=1.241
отрезок разбит на 10 частей ,
следовательно изменения значения функции происходит на каждом шаге на величину
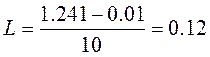
Тогда получаем, что
|
|
|
|
|
Только внутренние элементы матрицы |
|
|
|
|
Сделав такое предположение, мы получаем полностью заполненную матрицу u , при этом надо помнить , что это только начальные (стартовые
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.