Дифференциальные уравнения. Дифференциальные уравнения первого порядка и второго порядка

данному дифференциальному уравнению (14) нужно заменить функцию  y  единицей, а  производные    соответствующими степенями    при этом сохранить коэффициенты    

     Так,  для дифференциального уравнения    характеристическим будет уравнение    Для уравнения   – уравнение    Для всякого линейного однородного д.у. II с постоянными коэффициентами      характеристическим является  алгебраическое уравнение второй степени      (16) (квадратное уравнение).

     Пример. Составить линейное однородное д.у.II, зная характеристическое уравнение    Д.у. II будет  таким: 

 Решение квадратных уравнений

Обратимся к решению квадратных уравнений   

Формула корней квадратного уравнения:

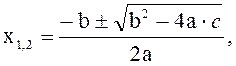
где  – дискриминант. Любое квадратное уравнение всегда имеет два корня (это известное положение высшей алгебры).

1)  Если 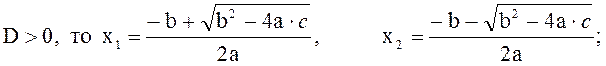 имеют

     место два различных действительных корня.

2)  Если 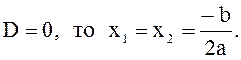    Имеем два равных действительных корня.

3) Если   то квадратное уравнение имеют два корня, но они не являются действительными числами. Эти корни называются комплексными числами.

     Обозначим   назовем мнимой единицей   Тогда число вида   где   действительные числа, называется  комплексным числом. Здесь   называется действительной частью,  мнимой частью комплексного  числа. Для всякого комплексного числа   существует комплексное число, ему сопряженное:   Так, для числа    сопряженным является число  Два комплексных числа    и   являются взаимно сопряженными. Покажем примеры решения квадратных уравнений.

     № 1.   

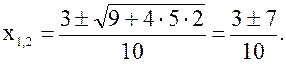
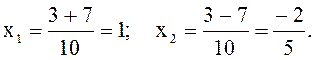
 различные действительные корни.

     № 2.

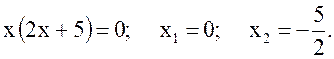
 различные действительные корни.

     № 3.  

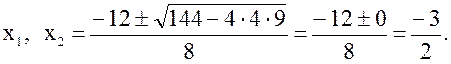
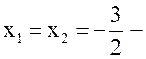 равные действительные корни.

     № 4. 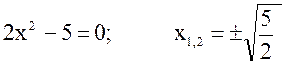  – различные корни.

     № 5.   

Уравнение имеет два комплексных корня, взаимно сопряженных, c действительной частью    и коэффициентом мнимой части 

     № 6.

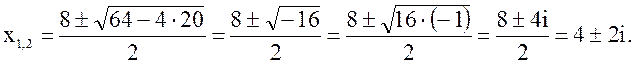
Уравнение   имеет  2  взаимно сопряженных  комплексных  корня:     где

 

     Заметим, что всякое алгебраическое уравнение степени  n   имеет ровно  n  корней, среди которых могут быть как действительные (различные или равные), так и комплексные (обязательно попарно взаимно сопряженные).

     № 7.   

Разложим   левую   часть   уравнения  на  множители: 

  Нужно решить три простейших уравнения:

Имеем четыре корня:

Решение однородных линейных дифференциальных уравнений

второго порядка с постоянными коэффициентами

 Дано  дифференциальное  уравнение     

При решении   характеристического уравнения      возможны три случая.

    1) Корни характеристического уравнения  (16) действительны и различны:    В этом случае частными решениями          будут функции

;    

при этом эти решения линейно независимы, т. к.

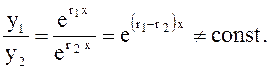
Тогда по теореме 1 общее решение уравнения (14) имеет вид

                                                                                                     (17)

где    произвольные  постоянные.

     2) Корни характеристического уравнения (16) действительны и   равны:   (обозначим  их  ). Тогда  имеет место  одно частное  решение  д.у. II   Доказано, что второе частное решение имеет вид      при этом  очевидно, что эти решения линейно независимы. Тогда общим решением  д.у. II будет

или                                                                                                (18)

3) Корни характеристического уравнения (16) комплексные сопряженные:

Тогда общее решение д.у. II  имеет вид

                                               .                                   (19)

Рассмотрим примеры.

     № 1.          

                 – характеристическое уравнение.

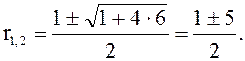
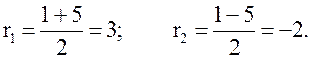
По формуле (17) находим общее решение дифференциального уравнения:

     № 2. 

             – характеристическое уравнение.

                                   

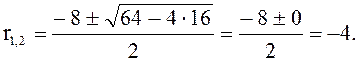
По формуле (18) получим общее решение дифференциального уравнения:

     № 3. 

                                      –характеристическое уравнение.

Уравнение имеет комплексные корни 

По формуле  (19)  общим  решением  будет

или    

     № 4. Найти частное решение уравнения     при  начальных условиях  

Характеристическое  уравнение:   

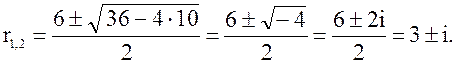
Общее решение –  

Найдем производную 

Подставив начальные условия     получим систему для определения  

                                

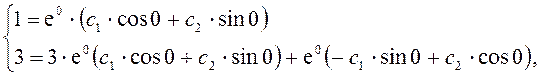
или

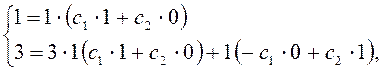
или

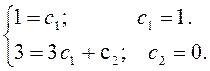
Подставив полученные значения     в общее решение, получим  – искомое частное решение.

     Проверка. Найдем   первую        и  вторую        производные функции   и  подставим в данное  дифференциальное уравнение:

 

  –верное равенство, т. е. частное решение найдено верно.

     Таким образом, решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами  совершается без операции  интегрирования функций (как в случае д.у.1) и полностью завершается посредством решения алгебраических квадратных уравнений. Аналогичный результат имеет место и для линейных однородных д.у. с постоянными коэффициентами  высших порядков.

 Примеры решения однородных линейных дифференциальных

уравнений высших порядков

     № 1. 

                – характеристическое уравнение

         

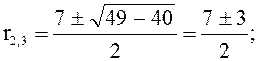
Общее решение:

или

     № 2.      

                     – характеристическое уравнение.

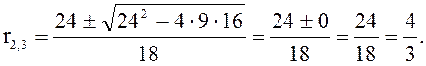
Общее решение:     или   .

     № 3.  

                         

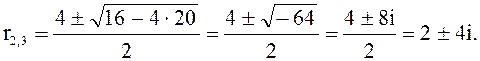
Общее решение: 

     № 4.  

                – характеристическое уравнение.

Положим 

                                 

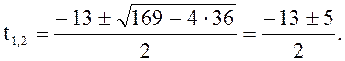
Общее решение уравнения:  

 Линейные неоднородные дифференциальные уравнения

 второго порядка

 Линейное неоднородное уравнение отличается от однородного  функцией в правой части. Линейное неоднородное уравнение имеет вид

а соответствующее ему линейное  однородное уравнение –

                                                                                                             

которое, как известно, решается с помощью характеристического уравнения (16)

                                                          

Сформулируем теорему о структуре общего решения неоднородного уравнения (13).

     Теорема 2. Общее решение неоднородного линейного дифференциального уравнения равно сумме  какого-либо частного решения этого уравнения и общего решения соответствующего однородного уравнения.

     Пусть  y– общее решение уравнения   (13)

какое-либо частное решение уравнения (13),

общее решение соответствующего однородного уравнения (14)

                                                                                                      

Тогда                                     

      Таким образом, основная задача при решении неоднородного линейного д.у. II состоит в нахождении какого-либо частного решения.

     Укажем один из методов нахождения частного решения  неоднородного уравнения , когда правая часть уравнения   имеет специальный вид. К таким функциям    относятся следующие функции: экспонента   многочлены  n-й степени относительно переменной  х     тригонометрические функции     а также их  произведения.

 Метод неопределенных коэффициентов

     Этот метод иначе называется методом подбора  частного решения    уравне-ния (13)  по виду правой части  .

 Пусть правая часть    уравнения

                                                                                                         

имеет вид   т. е. представляет собой  произведение экспоненты на многочлен, где    многочлен n-й  относительно  х. Тогда возможны следующие случаи.

1)  Число    не является корнем характеристического уравнения (16)

                                                                                                       

В этом случае частное решение нужно искать в виде 

где  многочлен той же степени, что и данный многочлен  , но с неопределенными коэффициентами.

2)  Число   есть простой (однократный) корень характеристического уравнения (т. е.    совпадает с одним корнем характеристического уравнения). В этом случае частное решение нужно искать в виде  .

3)  Число   есть двукратный  корень характеристического уравнения (т. е.   совпадает с двумя равными корнями характеристического уравнения). В этом случае  частное решение нужно искать в виде     Неизвестные (неопределенные) коэффициенты многочлена    находим из условия