Методы решения задач транспортного типа. Методы решения задач линейного и целочисленного программирования

элементы разрешающей строки (строка, в которой стоит разрешающий элемент) кроме самого разрешающего элемента умножаем на λ, а все элементы разрешающего столбца умножаем на –λ и записываем значения в нижние части клеток. В разрешающей строке выделяем все прежние элементы (стоящие в верхней части клеток) кроме разрешающего, а в разрешающем столбце – все новые (стоящие в нижней части клеток). В нижнюю часть клетки, не принадлежащей ни разрешающей строке, ни разрешающему столбцу, записываем произведение выделенных элементов и расположенной в строке и столбце, что и эти элементы.

Таблица 2.1 - Симплекс – таблица для прямой задачи

Базисные переменные	Свободный член		Свободные переменные
			X1		X2
Y1	88		8		11
		8		8/11		1/11
Y2	88		11		8
		-64		-64/11		-8/11
L	0		8		8
		-64		-64/11		-8/11

Чертим новую таблицу (Таблица 2.2)с новым набором свободных переменных. Меняем местами x₁ и y₂. Элементы разрешающих строки и столбца заменяем элементами, стоящими в нижних частях тех же клеток предыдущей таблицы. В остальных клетках новой таблицы записываем алгебраическую сумму элементов, стоящих в верхних и нижних частях соответствующих клеток прежней таблицы.

Таблица 2.2 - Симплекс – таблица для прямой задачи

Базисные переменные	Свободный член		Свободные переменные
			Y1		X2
Y1	42		-  7/10		78/10
		420/78		-  7/78		10/78
X1	6		1/10		6/10
		-252/78		42/780		-  6/78
L	-42		-  7/10		18/10
		-756/78		126/780		-  18/78

Чертим новую таблицу (Таблица 2.3)  с новым набором свободных переменных. Меняем местами x₂ и y₁. Элементы разрешающих строки и столбца заменяем элементами, стоящими в нижних частях тех же клеток предыдущей таблицы. В остальных клетках новой таблицы записываем алгебраическую сумму элементов, стоящих в верхних и нижних частях соответствующих клеток прежней таблицы.

Таблица 2.3 - Симплекс – таблица для прямой задачи

Базисные переменные	Свободный член		Свободные переменные
			Y1		Y2
Х1	264/57		-8/57		121/627
Х2	264/57		11/57		-8/57
L	-4224/57		-24/57		-264/627

Все элементы нижней строки новой таблицы отрицательны, значит оптимальное решение найдено. X1=264/57=4,6; X2=264/57=4,6; L=4224/57=74,1.

Результаты, полученные симплекс - методом и графически – близки.

Двойственный метод (Таблицы 2.4 – 2.6):

Решим задачу симплекс-методом. Для этого строим симплекс-таблицу и заполняем ее аналогично прямому методу, только работаем с уравнениями (5) – (7).

Таблица 2.4 - Симплекс – таблица для двойственной задачи

Базисные переменные	Свободный член		Свободные переменные
			Y1		Y2
X1	8		8		11
		8/11		8/11		1/11
X2	8		11		8
		-64/11		-64/11		-8/11
L	0		88		88
		-64		-64		-8

Таблица 2.5 - Симплекс – таблица для двойственной задачи

Базисные переменные	Свободный член		Свободные переменные
			Y1		X1
Y2	8/11		8/11		1/11
		-192/627		-8/57		64/627
X2	24/11		57/11		-8/11
		24/57		11/57		-8/57
L	-64		24		-8
		-6336/627		-264/57		2112/627

Таблица 2.6 - Симплекс – таблица для двойственной задачи

Базисные переменные	Свободный член		Свободные переменные
			X2		X1
Y2	264/627		-8/57		121/627
Y1	24/57		11/57		-8/57
L	-4224/57		-264/57		-264/57

Y1=264/627=0,42; Y2=24/57=0,42; L=46464/627=74,1.

Результаты, полученные симплекс - методом и результаты, полученные графически – близки.

2.6 Математическая постановка задачи линейного целочисленного программирования (ЛЦП)

Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами.

Таким образом, математическая модель задачи ЛЦП имеет следующий вид.

Найти минимальное значение линейной функции  ,

при ограничениях:

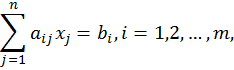
 где  – целые.

Задание для ЛЦП:

2.7 Графическая интерпретация задачи ЛЦП. Графический способ решения задачи ЛЦП

Задача ЛП имеет многогранник решений. Если наложить требование целочисленности, то допустимое множество решений задачи представляет собой совокупность изолированных целочисленных точек (График 2.3). Если добавить новые ограничения, связывающие внешние целочисленные точки, а затем в качестве многогранника решений использовать все выпуклое множество, ограниченное осями координат и новым контуром, то получим новую задачу ЛП со следующими свойствами:

1.  Новый многогранник решений содержит все целые точки, заключавшиеся в первоначальном многограннике решений; любая его угловая точка является целой;

2.  Так как линейная функция достигает оптимума в угловой точке многогранника решений, то построением такого многогранника и обеспечивается целочисленность оптимального решения.

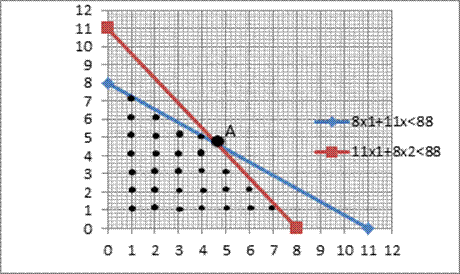
График 2.3 – Графический способ решения задачи ЛЦП

Так как мы решаем задачу максимизации, значит, оптимум находится в точке, при которой значение целевой функции максимально. Оптимальной является точка                 А (4,6; 4,6), .  

2.8 Решение задачи ЛЦП с помощью алгоритма Гомори

Находим опорное решение (п.2.5):

Таблица 2.7 - Симплекс – таблица для прямой задачи

Базисные переменные	Свободный член		Свободные переменные
			X1		X2
Y1	264/57		-8/57		121/627
Y2	264/57		11/57		-8/57
L	-4224/57		-24/57		-264/627

X1=264/57=4,6

X2=264/57=4,6

L=4224/57=74,1

Так как решение не является целочисленным, вводим дополнительное ограничение по формуле: .

Решаем задачу линейного программирования с дополнительным условием. Составляем симплекс-таблицу.

Таблица 2.8 - Симплекс – таблица для метода Гомори

Базисные переменные	Свободный член		Свободные переменные
			Y2		Y1
X2	264/57		-8/57		121/627
		288/627		8/11		-67/627
X1	264/57		11/57		-8/57
		-36/57		-1		8/57
Y3	36/57		11/57		-8/57
		36/11		57/11		-8/11
L	-4224/57		-24/57		-264/627
		864/627		24/11		-192/627

Таблица 2.9 - Симплекс – таблица для метода Гомори

Базисные переменные	Свободный член		Свободные переменные
			Y3		Y1
X2	3192/627		8/11		57/627
X1	4		-1		0
Y2	36/11		57/11		-8/11
L	-45600/627		24/11		-456/627

Так как решение не является целочисленным, вводим еще одно дополнительное ограничение, в которое входит нецелочисленная переменная x₂.

Таблица 2.10 - Симплекс – таблица для метода Гомори

Базисные переменные	Свободный член		Свободные переменные
			Y3		Y1
X2	3192/627		8/11		1/11
		-1/11		-8/11		-1
X1	4		-1		0
		0		0		0
Y2	36/11		57/11		-8/11
		8/11		64/11		8
Y4	1/11		8/11		1/11
		1		8		11
L	-45600/627		24/11		-456/627
		8/11		64/11		8

Таблица 2.11 - Симплекс – таблица для метода Гомори

Базисные переменные	Свободный член		Свободные переменные
			Y3		Y4
X2	5		0		-1
X1	4		-1		0
Y2	4		11		8
Y1	1		8		11
L	-72		8		8

Целочисленное решение найдено:

.

2.9. Найти решение задачи ЛЦП с помощью алгоритма ветвей и границ (алгоритм Ленг и Дойг).

Метод ветвей и границ:

Итерация 1:  , т.к. при условии  условия (2) выполняются. Основной список на 1 итерацию содержит одну задачу ЛП:

Задача 1 состоит из формул (1), (2) и (3).

Шаг 1: Выбираем первую задачу из основного списка.

Шаг 2: Решаем выбранную задачу и ищем оптимальное решение.

X1=264/57=4,6

X2=264/57=4,6

L=4224/57=74,1

Так как полученное оптимальное решение нецелочисленное, то выбираем произвольно переменную – х₁ и вносим в основной список 2 задачи  ЛП.

Задача 2: (1), (2),  

Задача 3: (1), (2),  

Принимаем целевую функцию в итерации 2 равной нулю и возвращаемся к шагу 1: .

Итерация 2:

Шаг 1: выбираем задачу №2.

Шаг 2: решаем задачу №2:

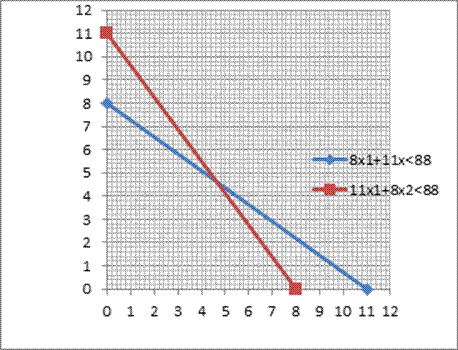
Она не имеет допустимого решения

Итерация 3:

Шаг 1: выбираем задачу №3.

Шаг 2: решаем задачу №3:

X1=4

X2=56/11=5.09

W=800/11=72.72

Так как решение нецелочисленное, то выбираем переменную х₂ , и вносим в основной список 2 задачи  ЛП.

Задача 4: (1), (2),  

Задача 5: (1), (2),  

Итерация 4:

Принимаем целевую функцию   и возвращаемся к шагу 1.

Шаг 1: выбираем задачу №4:

Шаг 2:  решаем выбранную задачу

X1=4

X2=5

W=72

Найденное  оптимальное решение  является целочисленным, значит