2009-09-16
Лекция 4
Линейное программирование
Алгебраическая формулировка задачи линейного программирования в общем виде
Требуется найти максимум или минимум линей функции n-переменных.
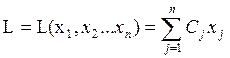 (1)
(1)
![]()
При ограничениях,
наложенных на переменные ![]() вида:
вида:
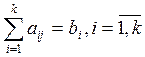 (2)
(2)
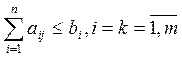 (3)
(3)
![]() (4)
(4)
При ограничения 2-4 поставленная задача оптимизация может принимать три случая:
Запись критерия и ограничений в разных задачи различается. Различие в записях условий задачи целесообразно сводить к канонической форме (далее КФ).
КФ задачи линейного программирования
Задачи линейного программирования (далее ЛП) следующим образом:
- найти минимум линейной формы 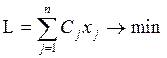 ;
;
- 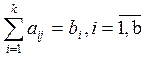 ; (5)
; (5)
- ![]() . (6)
. (6)
Из условий
1-4 видно, что для перехода к КФ необходимо от ограничений неравенств 3 перейти
к ограничениям равенства. В условия 3 введем дополнительные неотрицательные
переменные ![]() . Тогда ограничение 3 можно представить в
виде равенств:
. Тогда ограничение 3 можно представить в
виде равенств:
![]()
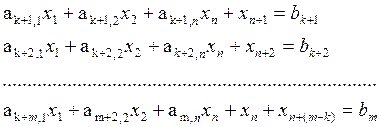 (7)
(7)
В линейную форму дополнительные переменные входят с нулевыми коэффициентами.
Если число неотрицательных
переменных ![]() , то общая задача уже сведена к КФ. Если
, то общая задача уже сведена к КФ. Если ![]() , то возможны два варианта:
, то возможны два варианта:
Такая запись в форме 5 приводит к общему росту числа переменных.
а) задача ЛП неразрешима;
б) общее количество переменных и ограничений сокращается.
Графическая интерпретация задач ЛП
Пример:
найти оптимальное решение, которое обращает в максимум (минимум) линейную
функцию семи переменных. ![]() при пяти уравнениях
ограничений:
при пяти уравнениях
ограничений:
![]() 1.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
Выбираем в
качестве свободных переменных ![]() и
и ![]() . Выразим через них базисные переменные
. Выразим через них базисные переменные ![]() .
.
По условию задачи все переменные должны быть неотрицательны. Имеем систему:
![]()
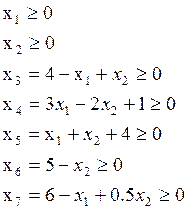
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.