Симплекс-метод решения задачи линейного программирования, страница 4

Значение целевой функции увеличилось: z⁽¹⁾ = 2. Это число является свободным членом ограничения (4`). В самом деле, так как небазисные переменные х<sub>2</sub> = х<sub>5</sub> =0, то из (4`) z = 2 (z - 0 + 0 = 2). Подстановкой плана в целевую функцию можно получить тот же результат
(-5*0 + 2*1 = 2).

Из ограничения (4`) видно, что план Х⁽¹⁾ тоже не является оптимальным. Значение z можно еще увеличить за счет увеличения х₂ .

Чтобы определить, до какого значения можно увеличить переменную х₂, и какую переменную следует вывести из базиса, снова по очереди рассмотрим ограничения.

В ограничение (1`) х₂ входит с отрицательным коэффициентом -0,5. Следовательно, при увеличении х₂ значение базисной переменной х₃, входящей в это ограничение, тоже будет увеличиваться (и это увеличение может происходить до бесконечности).

В ограничение (2`) входит базисная переменная х<sub>6</sub>. Если уменьшить ее до нуля, то, учитывая, что небазисные переменные х<sub>1</sub> = х<sub>4</sub> = х<sub>5</sub> = 0, получим 0,5х<sub>2</sub>      = 4 Û х<sub>2</sub> = 4/0,5 = 8. Следовательно, ограничение (2`) позволяет увеличить х₂ до 8 (за счет уменьшения х₆).

В ограничение (3`) переменная х₂ вообще не входит, следовательно, и оно позволяет увеличивать значение этой переменной до бесконечности.

Таким образом, самым жестким ограничением является второе, и мы увеличим х₂ до 8.

Следовательно, в новом опорном плане переменная х₂ станет базисной, а х₆ из базиса выйдет. Снова преобразуем систему методом Гаусса таким образом, чтобы столбец коэффициентов при х₂ стал единичным, причем единица должна стоять во втором ограничении (разрешающим столбцом будет столбец коэффициентов при х₂, а разрешающим ограничением – второе; разрешающий элемент равен 0,5).

Для этого обе части ограничения (2`) разделим на 0,5 (результат обозначим (2``)).

Из ограничения (1`) вычтем уравнение (2``), умноженное на (-0,5) (поскольку в ограничении (1`)  в разрешающем столбце стоит именно
(-0,5), а надо получить 0). Результат обозначим (1``).

Третье ограничение оставим без изменений, обозначив (3``) (поскольку х₂ в это ограничение не входит).

Из ограничения (4`) вычтем уравнение (2``), умноженное на (-1) (поскольку в ограничении (4`)  в разрешающем столбце стоит именно
(-1), а надо получить 0). Результат обозначим (4``).

1``) -х₁      + х₃ + х₄        + х₆                = 5

2``) 3х₁ + х₂    + 2х₄ - х₅ + 2х₆         = 8

3``) -3х₁          + 5х₄                    + х₇     = 7

4``) z + 3х₁          + 2х₄           + 2х₆         = 10

х_1-7 ³ 0

Этой системе можно поставить в соответствие новый опорный план Х⁽²⁾ = (0; 8; 5; 0; 0; 0; 7). Значение целевой функции увеличилось: z⁽²⁾ = 10.

Из ограничения (4`) видно, что значение целевой функции увеличить больше нельзя. Для этого пришлось бы уменьшить значения переменных х₁,  х₄ или х₆, а они и так равны нулю. Следовательно, Х⁽²⁾ – оптимальный план, а 10 – оптимум задачи.

3.2.2 Решение задачи в общем виде. Симплексная таблица

Вернемся к решению задачи в общем виде из раздела 3.2, начиная с исходного опорного плана Х = (b₁, b₂, . . . b_m, 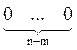). Обозначим z целевую функцию задачи. На исходном плане значение целевой функции 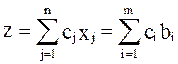, так как слагаемые, соответствующие небазисным переменным, обратятся в 0.

Для применения симплекс-метода к системе необходимо приписать еще одно ограничение - критериальное: z - 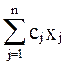 = 0.

В решенном примере это было четвертое ограничение. Поскольку в этом примере базисные переменные исходного опорного плана (х_5-7) не входили в целевую функцию, то и в критериальное ограничение они не вошли. В общем случае это не так. Например, если бы задача имела вид:

max -5х₁ + 2х₃

-2,5х₁ – 0,5х₂ + х₃    + 0,5х₅                                = 1

1,5х₁ + 0,5х₂               + х₄ - 0,5х₅ + х₆      = 4

-3х₁                             + 5х₄                      + х₇           = 7

х_1-7 ³ 0

то в качестве базисных в исходном опорном плане следовало бы взять переменные х₃, х₆ и х₇. Одна из них - х₃ - входит в целевую функцию. Уравнение z - 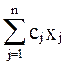 = 0 здесь приняло бы вид: z + 5х₁ - 2х₃ = 0. Чтобы увеличить z, здесь следовало бы увеличить х₃. Но переменная х₃ и так является базисной, уже равна 1, и из ограничений следует, что увеличить ее до большего значения невозможно. Такое затруднение возникло из-за того, что после добавления критериального ограничения столбцы коэффициентов перестали быть единичными. Базисные переменные должны входить в него с нулевыми коэффициентами, а в последней задаче это не так.