Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 8

          Совокупность алгебры и отношений R={r₁, r₂,..} называют алгебраической системой, т.е. A_сист.=<X, F, R>.

Например, если даны отношения £(x_i, x_i) или Í(X_i, X_j), т.е. задан частичный порядок на множестве X, то A=<X, F, £> и A=<X, F, Í> есть алгебраические системы.

Если элементы множества, упорядоченного отношением £(x_i, x_i), принимают значения только на множестве {0, 1}, то операции поиска верхней и нижней граней на таком множестве формируют булеву алгебру. Тогда

Sup X=(x_iÚx_j) есть операции дизъюнкции – “Ú”, а Inf X=(x_i×x_j) есть операции конъюнкции конъюнкции – “×”.Поиск дополнения значения элемента x_i на множестве {0, 1} есть унарная операция –отрицание - `x_i.

Дизъюнкция (x₁Úx₂) есть бинарная операция, значение которой равно 0 в том и только в том случае, когда оба операнда имеют значение 0.             

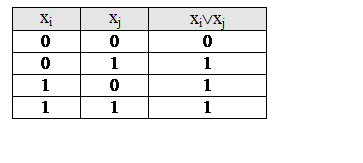Префиксная схема этой операции имеет вид: f(x_i, x_j)=disjunct(х_i, х_j).                   Операцию дизъюнкции можно распространить на произвольное число элементов множества X. Например,

f(х₁, х₂,..х_n)=(х₁Úх₂Ú...Úх_n)=_i=1Úⁿх_i.

          Конъюнкция (x₁×x₂) есть бинарная операция, значение которой равно 1 в том и только в том случае, когда оба операнда имеют значение 1.

Префиксная схема этой операции имеет вид: f(x_i, x_j)=conjunct(х₁, х₂).

Операцию конъюнкции можно распространить на произвольное число элементов множества.

Например, f(х₁, х₂, ..х_n)=(х₁×х₂×..×х_n)=

_i=1&ⁿх_i, где _i=1&ⁿ - символ конъюнкции

 для 1£i £n.

Отрицание `x есть унарная операция, значение которой противоположно значению операнда.

x	f(x)=`x
0	1
1	0

Префиксная схема этой операции имеет вид:       f(x)=not(x).

Операцию отрицания можно распространить на произвольные формулы булевой алгебры. 

Например, F_i=(х₁Úх₂Ú...Úх_n) или F_j=(х₁×х₂×...×x_n).

Операции поиска верхней и нижней граней на множествах, упорядоченных отношением  Í(X_i;X_j), есть операции объединения - È и пересечения - Ç, т. е.

Sup X=(X_iÈX_j) и Inf X=(X_iÇX_j). Поиск элементов множества X_j, не принадлежащих множеству X_i, есть унарная операция – дополнение - ùX_i, т. е. ùX_i={x| xÏX_i и xÎX_j}.

1. 5 Алгебра множеств

Две бинарные операции (È и Ç) и одна унарная операция (ù ), заданные на булеане универсального множества - Â(U), формируют алгебру множеств, т. е.

A_множ.=<Â(U); ù; È; Ç >,

где Â(U) – носитель алгебры,

F={ù; È; Ç}- сигнатура алгебры, где ù - символ унарной операции –дополнения, È - символ бинарной операции – объединения, Ç -символ бинарной операции - пересечения.

Непосредственно из определения граней упорядоченного множества подмножеств следуют основные законы алгебры множеств:

·  коммутативности: (AÈB)=(BÈA) и (AÇB)=(BÇA);

·  ассоциативности: AÈ(BÈC)=(AÈB)ÈC и AÇ(BÇC)=(AÇB)ÇC;

·  идемпотентности: AÇA=A и AÈA=A;

·  поглощения: AÇ(AÈB)=A и AÈ(AÇB)=A;

·   дистрибутивности: AÈ(BÇC)=(AÈB)Ç(AÈC) и                              AÇ(BÈC)=(AÇB)È(AÇC);

·  “третьего не дано” AÈùA=U;

·  противоречия: AÇùA=Æ.

·  двойного отрицания: ù (ùA)=A.

Рассмотрим исполнение отдельных операций над подмножествами A, B, C множества Â(U). Для изображения исполнения отдельных операций обозначим  прямоугольником универсальное множество U, а внутри него - кругами подмножества A, B и C. Заштрихованная область будет представлять результат исполнения операции. Такое изображение называют кругами Эйлера.

Объединение множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному множеству А или В, т.е. С=(АÈВ)={x| xÎA или xÎB}.    

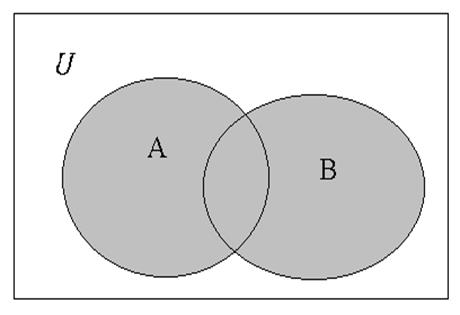Операторная запись объединения имеет вид: С=union(A, B).

Если В=Æ, то АÈВ=АÈÆ=А.

Если B=U, то АÈВ=АÈU=U.

Если АÍС и ВÍС, то АÈВÍС.

Рис. 2 Объединение множеств A и B.

Пример: Пусть даны множества A={a, b, c}, B={b, c, d, e}. Найти C= (АÈВ).