Полезность необходимого условия устойчивости заключается в возможности выявления неустойчивых систем по виду характеристического уравнения: если в уравнении встречаются отрицательные коэффициенты, либо отсутствуют некоторые из них, то соответствующая система является неустойчивой (однако, из положительности всех коэффициентов характеристического уравнения нельзя сделать вывод об устойчивости системы).
При n≤2 необходимое условие устойчивости является и достаточным, что следует из вида решений характеристических уравнений для систем 1-го и 2-го порядков. Учитывая то обстоятельство, что устройства радиоавтоматики в своем большинстве имеют невысокую размерность, такой критерий устойчивости оказывается весьма полезным.
Применим необходимое
условие устойчивости для характеристического уравнения системы 2-го порядка: 
(см. пример разд. 2.1). Из положительности коэффициентов
характеристического уравнения Kτ>0 и K>0 получаем
известные нам ограничения на параметры устойчивой СУ: K>0, τ>0.
2. Критерий Рауса-Гурвица.
При n>2 необходимое условие устойчивости следует дополнить неравенствами, полученными английским математиком Э. Раусом (1877 г.) и немецким математиком, профессором Цурихского университета А. Гурвицем (1895 г.). Заметим, что для случая n=3 такие неравенства были получены русским инженером И.А. Вышнеградским в 1876 г. Результаты Рауса и Гурвица представлены в различной форме, причем в случае n<5 проще использовать результаты Гурвица. Уравнение (2.8) удобно привести к виду:
(2.10)
где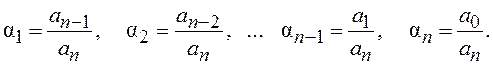 
Далее из коэффициентов характеристического уравнения (2.10) составляется матрица:
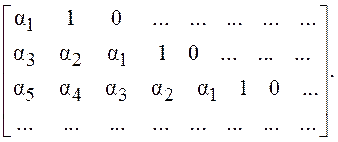(2.11)
Правило составления матрицы
следующее. На главной диагонали располагаются коэффициенты характеристического
уравнения (2.10), после чего в каждой строке вправо добавляют коэффициенты с
убывающими индексами и влево – возрастающими индексами (если индекс равен нулю –
записывают единицу, для отрицательных индексов и индексов, превышающих n,
записывают ноль).
Затем из элементов матрицы (2.11), расположенных симметрично
относительно главной диагонали, составляют n определителей Гурвица:
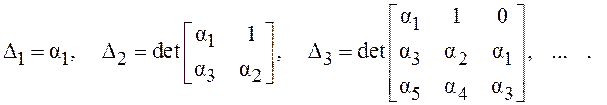
Формулировка критерия Рауса-Гурвица: для обеспечения устойчивости системы n-го порядка необходимо и достаточно, чтобы все n определителей Гурвица были положительны.
Поскольку 
и 
с учетом необходимого условия
устойчивости необходимо вычислять только (n-2) определителя и решать
систему неравенств:
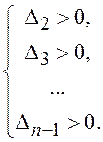
В качестве примера
рассмотрим систему с ПФ в разомкнутом состоянии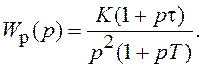 
Характеристическое уравнение этой системы имеет вид:
Из необходимого условия устойчивости следует: T>0, K>0, τ>0. Приводим характеристическое уравнение к виду:
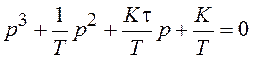, записываем матрицу:
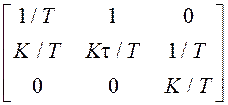и из ее элементов составляем три определителя
Гурвица, которые должны быть положительными:
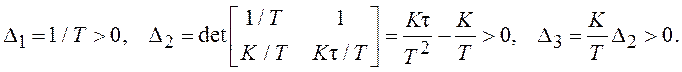
Из условия Δ2>0 находим дополнительное ограничение на параметры системы: τ>T.
3. Критерий Михайлова.
Этот критерий предложен русским ученым А.В. Михайловым в 1938 г. Левая часть характеристического уравнения с заменой p на jω:
называется характеристическим
комплексом. Отображение характеристического комплекса на комплексной плоскости
в виде годографа называют кривой Михайлова.
Формулировка критерия Михайлова: для обеспечения устойчивости системы n-го порядка необходимо и достаточно, чтобы кривая Михайлова начиналась (при ω=0) на положительной части вещественной оси и, с увеличением частоты ω, огибала начало координат, проходя последовательно n квадрантов против часовой стрелки.
Критерий Михайлова удобен тем, что для проверки устойчивости необязательно строить кривую Михайлова целиком. Достаточно найти точки пересечения вещественной и мнимой осей этой кривой.
В качестве примера
рассмотрим систему с ПФ в разомкнутом состоянии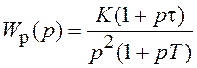 
и характеристическим комплексом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.