Оптимизация систем радиоавтоматики. Комплексные системы радиоавтоматики, страница 3

            Решение уравнения Винера-Хопфа в частотной области можно получить для случайных процессов со спектральной плотностью, описываемой дробно-рациональной функцией 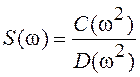. В этом случае  физически реализуемая передаточная функция оптимального фильтра  равна

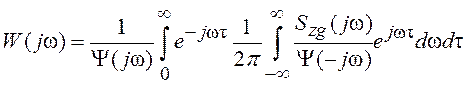,                      (5.9)

где ;  – спектральная плотность процесса  ;  – взаимная спектральная плотность процессов  и .

            Для нахождения оптимального фильтра требуется выполнить разложение функции  на два сомножителя  и , то есть выполнить факторизацию спектра. Процесс  с дробно-рациональным спектром  формируется с помощью фильтра с коэффициентом передачи , на вход  которого поступает белый шум с единичной спектральной плотностью.

            В радиотехнических системах сообщение  и помеха  не коррелированны, СПМ помехи , а спектральная плотность случайного процесса  имеет вид . Тогда из выражения (5.9) можно получить

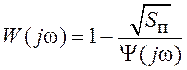.                                                (5.10)

            Действие оптимального фильтра, построенного в соответствии с выражением (5.10), можно объяснить с помощью эквивалентной схемы (рис. 5.6).

Процесс , содержащий сумму полезного воздействия и помехи, формируется с помощью фильтра  из белого шума  с единичной спектральной плотностью. Нижняя часть схемы содержит выбеливающий фильтр  и вырабатывает оценку шума . Оценка полезного сообщения строится как .

            Таким образом, решение задачи оптимальной фильтрации по критерию минимума среднего квадрата ошибки сводится к нахождению функции , которая позволяет найти структуру и оптимальные параметры стационарного фильтра. В этом фильтре минимум среднего квадрата ошибки достигается в установившемся режиме при . Если фильтр реализуется как система с обратной связью, из выражения (5.9) получим функцию передачи разомкнутого контура .

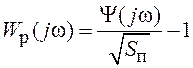.                                           (5.11)

            Пример 5.1. Построим оптимальный линейный фильтр для случайного процесса  со спектральной плотностью  при действии помехи в виде белого шума  со спектральной плотностью . Спектральная плотность . Факторизация спектра имеет вид

, .

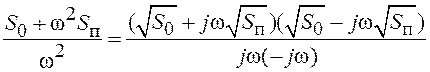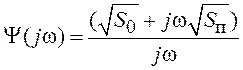            Таким образом ,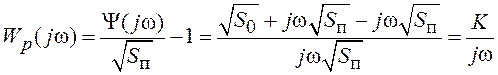

где  .

5.4. Линейный фильтр Калмана в непрерывном времени

            При построении оптимальных фильтров с переменными параметрами используется описание случайных процессов во временной области с помощью дифференциальных или разностных уравнений.

            Для представления состояния системы в непрерывном времени используем дифференциальное уравнение вида (3.41).

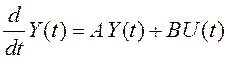,  ,                                (5.12)

где  – -мерный вектор;  – матрица размером ;  – матрица размером ;  – случайный -мерный вектор белого гауссовского шума с нулевым средним и диагональной корреляционной матрицей .

            Формирование наблюдения определяется уравнением, подобным (3.42).

,                                                 (5.13)

где  – -мерный вектор;  – матрица размером ;  – случайный -мерный вектор белого гауссовского шума с нулевым средним и корреляционной матрицей .  

            При проектировании оптимального фильтра предполагается, что на вход фильтра (рис. 5.7) поступает вектор наблюдения , формируемый в соответствии с выражениями (5.12) и (5.13). Оптимальный фильтр должен вырабатывать несмещенную оценку  с минимальной среднеквадратичной ошибкой.

 Условия формирования несмещенной оценки исследованы в разделе 3.9. В соответствии с выражением (3.46) уравнение оценки имеет вид

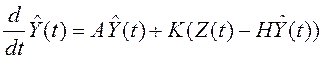,  ,                          (5.14)

где  – матрица размером .

Вычислим вектор ошибки  и используя (3.45) составим дифференциальное уравнение для корреляционной матрицы вектора ошибки.

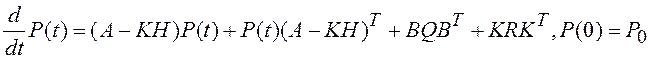.      (5.15)  

Выражение (5.15) позволяет определить корреляционную матрицу ошибки при произвольном значении коэффициента . Выполним оптимизацию его значения по минимуму следа корреляционной матрицы 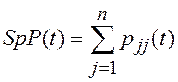. Для этого вычисляем градиент следа матрицы  по   и приравниваем его нулю.

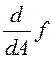Градиент скалярной величины  по матрице  размером  обозначается  и представляет собой матрицу такого же размера, заполненную производными по элементам матрицы . При вычислении градиента симметрической матрицы  используем следующие правила.