













Оператор Фурье на конечном интервале.
Рассмотрим кроме основного
пространства L2
два подпространства D и В. Элементами D являются финитные
функции, отличные от нуля лишь на промежутке [–T/2, T/2] и
получаемые из функций, принадлежащих L2 с помощью оператора проектирования D,
т. е. 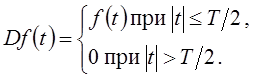 . Этот оператор называют оператором
временного селектирования или стробирования.
. Этот оператор называют оператором
временного селектирования или стробирования.
Элементами пространства В
являются функции с финитным спектром, у которых преобразование Фурье
тождественно равно нулю, если |w| > W. Во временной области действие этого
оператора описывается сверткой исходной функции f(t) и импульсной
характеристики h(t) идеального фильтра нижних частот (ФНЧ).
Импульсная характеристика ФНЧ имеет вид 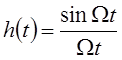 и
действие оператора В во временной области можно записать как
и
действие оператора В во временной области можно записать как ![]()
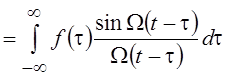 . Рассматривая
произведение операторов B и D (последовательное действие),
приходим к оператору Фурье на конечном интервале
. Рассматривая
произведение операторов B и D (последовательное действие),
приходим к оператору Фурье на конечном интервале 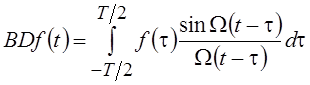 . В
качестве параметра этого оператора выступает коэффициент
. В
качестве параметра этого оператора выступает коэффициент 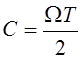 . В силу симметрии ядра оператор BD
является самосопряженным, поэтому его собственные функции, являющиеся решениями
уравнения Фредгольма
. В силу симметрии ядра оператор BD
является самосопряженным, поэтому его собственные функции, являющиеся решениями
уравнения Фредгольма 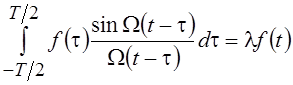 образуют ортонормальную систему
образуют ортонормальную систему ![]() полную в В.
полную в В.
Так как оператора BD
является положительно определенным, то его собственные значения положительны и
образуют убывающую последовательность l0 > l1 > … > ln > .…
Собственное значение lk равно энергии собственной
функции ![]() в интервале [–T/2, T/2], т.
е.
в интервале [–T/2, T/2], т.
е. 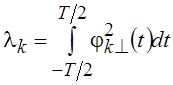 .
.
Система функций ![]() помимо ортонормальности на всей оси
помимо ортонормальности на всей оси 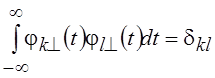 , где dkl – символ
Кронекера, равный 1, если k = l и 0, если k ¹ l, ортогональна на промежутке [–T/2,
T/2]
, где dkl – символ
Кронекера, равный 1, если k = l и 0, если k ¹ l, ортогональна на промежутке [–T/2,
T/2] 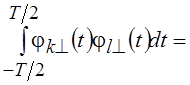
![]() .
Поэтому функции
.
Поэтому функции ![]() называют функциями с двойной
ортогональностью.
называют функциями с двойной
ортогональностью.
С оператором BD связано решение задачи об отыскании финитного сигнала (импульса) длительностью Т, имеющего в полосе частот [–W, W] максимальную долю полной энергии. Эта задача имеет большое значение для радиотехники, так как позволяет найти импульсный сигнал, имеющий минимум энергии вне заданной полосы частот (минимальное внеполосное излучение).
Итак, мы хотим определить форму импульса s(t), тождественно равного нулю вне интервала [–T/2, T/2], у которого энергия в полосе частот [–W, W]
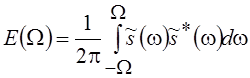 (5.8)
(5.8)
максимальна[*]
или, точнее, составляет максимальную долю полной энергии 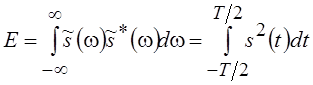 , которую мы, не снижая общности задачи,
будем считать равной единице, т. е. Е = 1. Так как
, которую мы, не снижая общности задачи,
будем считать равной единице, т. е. Е = 1. Так как 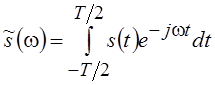 , то (5.8) можно записать следующим
образом:
, то (5.8) можно записать следующим
образом: 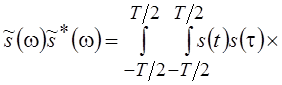
![]() и после подстановки в
(5.8) и интегрирования получим
и после подстановки в
(5.8) и интегрирования получим 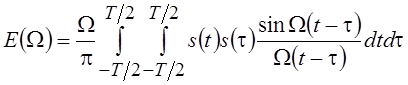 .
.
Таким образом,
необходимо решить следующую задачу. При заданных Т и W и условии 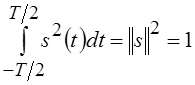 обеспечить
выбором функции s(t) максимум функционала
обеспечить
выбором функции s(t) максимум функционала 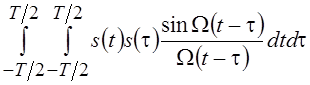 ,
который, как мы уже отмечали выше, является положительно определенной
квадратичной формой (BDs, s). Множитель
,
который, как мы уже отмечали выше, является положительно определенной
квадратичной формой (BDs, s). Множитель ![]() перед
функционалом опущен, так как он не влияет на решение поставленной задачи.
Рассмотрим вначале более общую задачу.
перед
функционалом опущен, так как он не влияет на решение поставленной задачи.
Рассмотрим вначале более общую задачу.
Пусть требуется
обеспечить экстремум квадратичной форме![]() где А
– самосопряженный положительно определенный оператор, при ограничении
где А
– самосопряженный положительно определенный оператор, при ограничении ![]() . Это задача на условный экстремум. В
соответствии с методом неопределенных множителей Лагранжа эта задача сводится к
отысканию безусловного экстремума функционала
. Это задача на условный экстремум. В
соответствии с методом неопределенных множителей Лагранжа эта задача сводится к
отысканию безусловного экстремума функционала ![]() , где l – неопределенный множитель Лагранжа.
, где l – неопределенный множитель Лагранжа.
Пусть ![]() – искомый вектор, для которого достигается
экстремум
– искомый вектор, для которого достигается
экстремум ![]() . Представим произвольный вектор
. Представим произвольный вектор ![]() в форме
в форме ![]() , где
, где ![]() – произвольный вектор, а a – числовая переменная. Этот прием позволяет
свести задачу исследования на экстремум функционала к аналогичной задаче для
функции переменной a, что неизмеримо
проще. Подставляя
– произвольный вектор, а a – числовая переменная. Этот прием позволяет
свести задачу исследования на экстремум функционала к аналогичной задаче для
функции переменной a, что неизмеримо
проще. Подставляя ![]() в
в ![]() и выполняя
действия в соответствии с аксиомами скалярного произведения, получим
и выполняя
действия в соответствии с аксиомами скалярного произведения, получим
![]()
![]() .
.
Мы предполагали,
что оператора А определен в вещественном пространстве и a – вещественная переменная. Можно
утверждать, что функционал Лагранжа ![]() , рассматриваемый как
функция a имеет экстремум при a = 0, так как в этом случае
, рассматриваемый как
функция a имеет экстремум при a = 0, так как в этом случае ![]() и достигается экстремум. Записывая необходимое
условие экстремума
и достигается экстремум. Записывая необходимое
условие экстремума 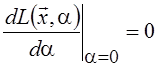 , после элементарных преобразований
и введения единичного оператора Е получим
, после элементарных преобразований
и введения единичного оператора Е получим ![]() . Так
как
. Так
как ![]() – произвольный ненулевой вектор, то
выполнение записанного условия возможно только если
– произвольный ненулевой вектор, то
выполнение записанного условия возможно только если ![]() или
или ![]() . Таким образом, экстремум квадратичной
формы
. Таким образом, экстремум квадратичной
формы ![]() при условии
при условии ![]() достигается
на собственных векторах оператора А. Само экстремальное выражение
достигается
на собственных векторах оператора А. Само экстремальное выражение ![]() равно собственному значению, отвечающему
собственному вектору
равно собственному значению, отвечающему
собственному вектору ![]() . Напомним, что для положительно
определенного самосопряженного оператора собственные значения положительны.
. Напомним, что для положительно
определенного самосопряженного оператора собственные значения положительны.
Таким образом, для
нашей задачи отыскания импульса с максимальной концентрацией энергии в полосе
[–W, W]
необходимо найти собственную функцию, отвечающую наибольшему собственному
значению, а так как собственные значения нашего оператора образуют убывающую
последовательность l0 > l1 > … > ln > …, то это
функция ![]() .
.
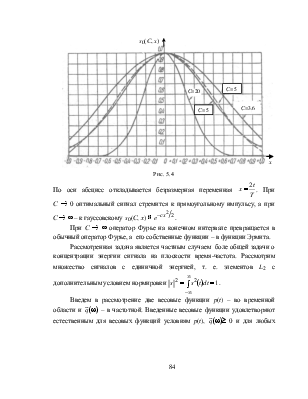
На рис. 5.4
приведены заимствованные из [10] графики оптимальных сигналов, построенные для
разных значений параметра 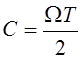 с нормировкой s0(С, 0) = 1.
с нормировкой s0(С, 0) = 1.
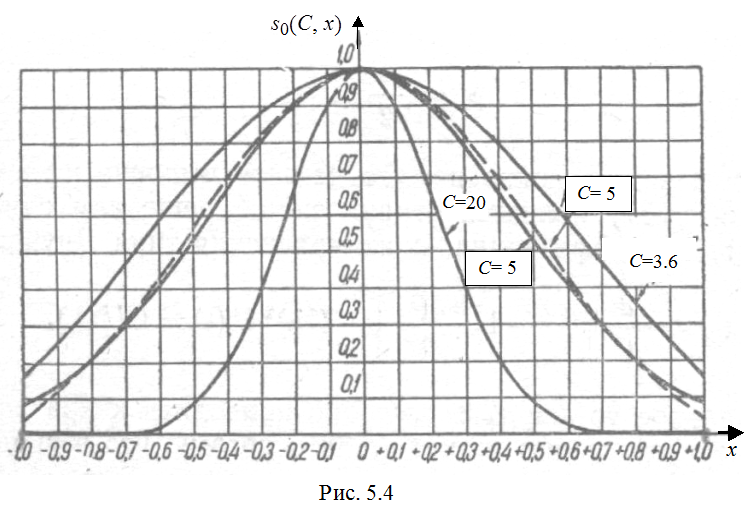
По
оси абсцисс откладывается безразмерная переменная 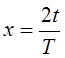 . При
. При
С ® 0 оптимальный сигнал
стремится к прямоугольному импульсу, а при
С ® ¥ – к гауссовскому s0(С, х) ![]() .
.
При С ® ¥ оператор Фурье на конечном интервале превращается в обычный оператор Фурье, а его собственные функции – в функции Эрмита.
Рассмотренная
задача является частным случаем боле общей задачи о концентрации энергии
сигнала на плоскости время-частота. Рассмотрим множество сигналов с единичной
энергией, т. е. элементов L2 с дополнительным условием нормировки 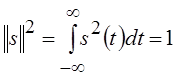 .
.
Введем в
рассмотрение две весовые функции р(t) – во временной области и ![]() – в частотной. Введенные весовые функции
удовлетворяют естественным для весовых функций условиям р(t),
– в частотной. Введенные весовые функции
удовлетворяют естественным для весовых функций условиям р(t), ![]() ³ 0
и для любых
³ 0
и для любых
s(t), ![]() Î
L2
энергетические функционалы
Î
L2
энергетические функционалы 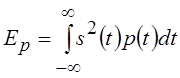 и
и 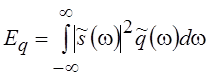 конечны.
конечны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.