Линейные операторы и функционалы. Часть 2, страница 3

Раскрывая неопределенность при w = w₀, получим: 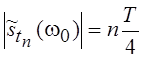, т. е. значение амплитудно-частотного спектра на частоте w₀ со временем линейно нарастает. На рис. 5.3 представлен заимствованный из замечательной книги [9] текущий спектр синусоиды, представленный в виде рельефа. По горизонтальной оси отложена нормированная относительно w₀ частота w, т. е. 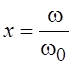. По оси, перпендикулярной плоскости чертежа, отложено число полупериодов синусоиды или время t. По оси ординат откладываются значения . Симметричная часть функции , соответствующая w < 0, опущена.

Пользуясь полученными результатами, легко установить, что спектр амплитудно-модулированного колебания

 ,

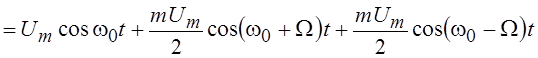где m – коэффициент амплитудной модуляции, 0 £ m £ 1, а W – частота модулирующего колебания, для w > 0 имеет вид:

.

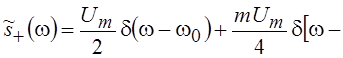
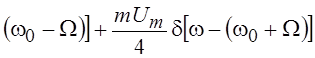Аналогичное выражение имеет место для w < 0:

.

Таким образом, спектр амплитудно-модулированного колебания при гармоническом законе модуляции содержит три линии, три дискретных частоты: несущую w₀ и две боковых (w₀+W) и (w₀–W).

Развитием понятия текущий спектр является переход к мгновенному спектру, который оказывается полезным при описании работы синтезаторов спектра и при изучении процессов, параметры которых меняются во времени.

Простейшее определение мгновенного спектра  дается на основе "скользящего" интегрирования 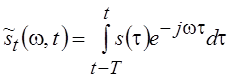. Более общее определение связано с введением весовой функции р(t). При этом определение мгновенного спектра принимает вид 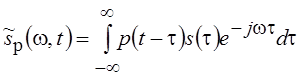. Приведенное выше определение есть частный случай данного, если положить p(x)= = 1(x + T) – 1(x), где 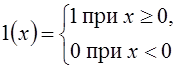 – уже знакомая нам функция единичного скачка.

Используя определение для текущего спектра (5.6), мгновенный спектр можно представить в виде приращения текущего спектра за промежуток времени Т: .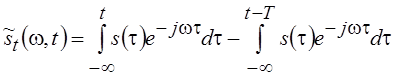

При малом Т это приращение может быть выражено через производную текущего спектра по времени 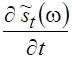, т. е. 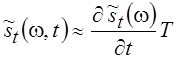. Часто более удобным является предложенный Пэйджем мгновенный спектр мощности 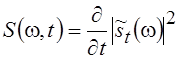, где  – текущий спектр.

Интеграл от этой функции по всем частотам дает мгновенную мощность сигнала s(t), т. е. 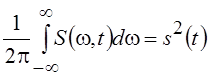, а интеграл по времени по всему прошлому дает квадрат модуля текущего спектра .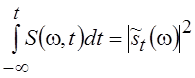

Преобразование Фурье используется для определения понятия кепстр сигнала 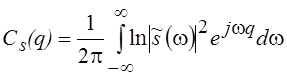, где  – амплитудный спектр сигнала s(t). Переменная q, имеющая размерность времени, в зарубежной литературе называют "quefrency", что по-русски дает не очень благозвучный термин "сачтота". Для того, чтобы обеспечить сходимость записанного интеграла, пределы интегрирования делают конечными, охватывающими частотную область, в которой сконцентрирована основная энергия сигнала. Основное свойство кепстра, обусловившее его использование в задачах анализа и синтеза речи, при исследовании радиолокационными методами среды распространения сигнала, заключается в том, что кепстр сигнала s(t), полученного как свертка функций f(t) и g(t) равен сумме кепстров C_f(q) и C_g(q). В самом деле, преобразование Фурье свертки f*g равно произведению спектров сворачиваемых сигналов , а 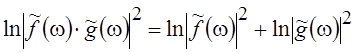 и с учетом линейности преобразования Фурье получаем C_s(q) = C_f (q) + C_g(q).