Корреляционные и спектральные характеристики случайных процессов, страница 2

СПМ и КФ данного процесса равны, соответственно:

,

.

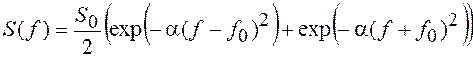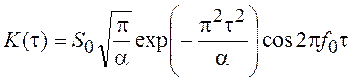Дисперсия будет такая же, как в предыдущем примере. Графики СПМ и КФ приведены на рис. 24, д.

6.  Случайный процесс с “Лоренцевским” энергетическим спектром.

В приложениях часто встречается СП, у которого 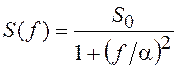. Корреляционная функция такого процесса имеет вид . Параметр a определяет ширину спектра и время корреляции.

Например, 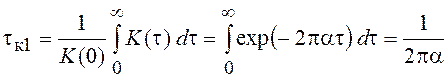. Графики СПМ и КФ приведены на рис. 24, е.

7.  В качестве последнего примера найдем КФ и СПМ квазидетерминированного процесса , где U_m и w₀ – известные амплитуда и несущая частота, а q – случайная величина с ПВ

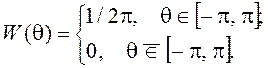
Математическое ожидание этого СП равно

.

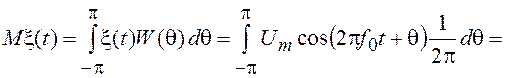
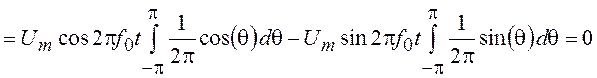КФ также можно найти с помощью усреднения по q:

.

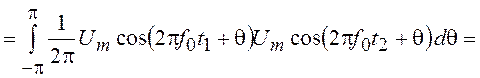
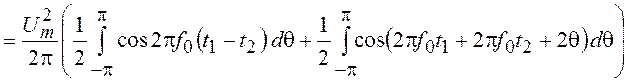Второй интеграл равен нулю, следовательно, .

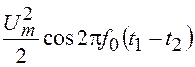Таким образом мы установили, что рассматриваемый процесс является стационарным в широком смысле, так как его среднее значение равно нулю и не зависит от t, а КФ зависит лишь от разности t₁ – t₂. СПМ рассматриваемого процесса имеет вид 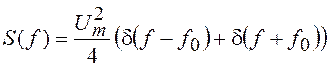 . Графики S(f) и K(t) приведены на рис. 24, ж.

Как и для детерминированных сигналов, для СП можно выделить класс узкополосных СП, удовлетворяющих условию Df << f₀, где Df – ширина СПМ, а f₀ – ее центральная частота.

Для узкополосных СП спектральную плотность S(f) можно представить в виде двух неперекрывающихся, как это показано на рис. 25, в, д, слагаемых:

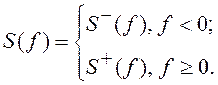
Тогда 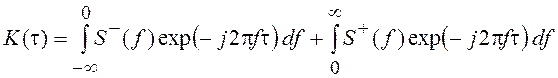. Если ввести в рассмотрение функции  и , представляющие собой части СПМ  и 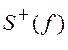, смещенные на величину f₀ соответственно вправо и влево (см. рис. 24, ж), то получим:

.

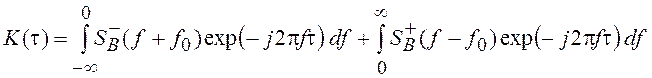Выполняя в первом интеграле замену переменной  f + f₀ = x, а во втором
f – f₀= x, и учитывая, что  и  при | f| > f₀ пренебрежимо малы, получим после несложных преобразований следующее выражение для КФ узкополосного процесса:

.

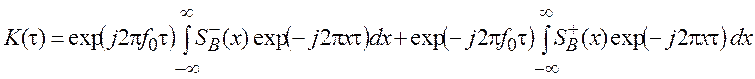В силу четности СПМ S(f) выполняется условие  =  (см. рис. 25) и выражение для КФ можно окончательно записать в форме

,

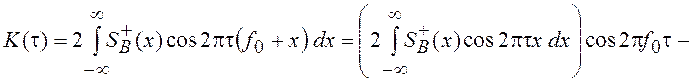
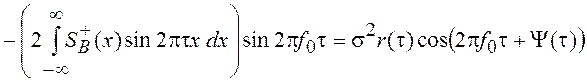где  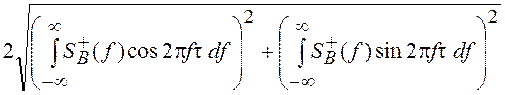– огибающая КФ узкополосного процесса, а Y(t) – фаза КФ, определяемая выражением

.

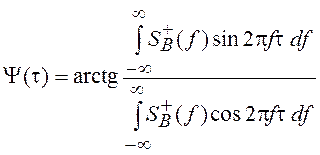Огибающая КФ является четной функцией t, а Y(t) – нечетная функция.

Если СПМ симметрична относительно частот  ± f₀, то  = = =  будут четными функциями, следовательно, будет иметь место равенство 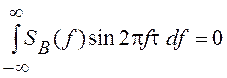 и КФ узкополосного процесса примет вид:

K(t) = , где  .

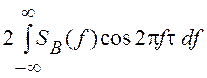Таким образом, КФ узкополосного СП имеет вид радиоимпульса с огибающей  и высокочастотным заполнением, имеющим в общем случае угловую модуляцию по закону

,

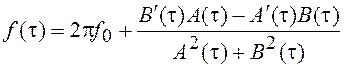где 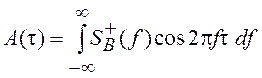 и 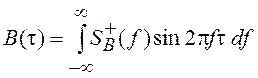. Если СПМ симметрична относительно частот ± f₀, то ,  и угловая модуляция КФ отсутствует.

Комплексные случайные процессы.

В некоторых задачах приходится сталкиваться с комплексным случайным процессом x(t) = z(t) + jh(t), где z(t) и h(t) – вещественные случайные процессы. Процесс x(t) будет полностью определен, если для любых п и t₁, t₂, …, t_n  можно задать совместную ФР F(x₁, y₁, x₂, y₂, …, x_n, y_n; t₁, t₂,
…, t_n) = 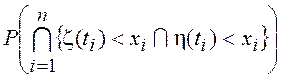. Среднее значение, корреляционная функция и дисперсия равны, соответственно:

Мx(t) = Мz(t) +Мjh(t);

;

М₂x(t) = .

Случайные процессы с дискретным спектром.

Рассмотрим СП вида x(t) =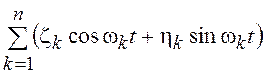, где z_k и h_k – случайные, а w_k – детерминированные величины. Выясним, при каких условиях данный СП будет стационарным в широком смысле. Во-первых, среднее значение Мx(t) не должно зависеть от времени. Это возможно только тогда, когда Мz_k = Мh_k = 0, k = 1, 2, …, n. Во-вторых, корреляционная функция 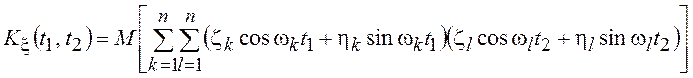 должна зависеть от разности t₁ – t₂ = t. Для этого должны выполняться следующие условия: М₂z_k = М₂h_k = , , k¹ l.

При выполнении этих условий КФ процесса x(t) принимает вид

.

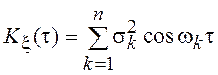Спектральная плотность, соответствующая записанной КФ, будет представлять собой сумму дельта-функций на дискретных частотах ±w_k:

.

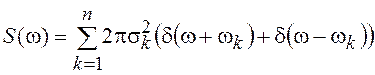При k = 1 получаем гармоническое колебание

x(t) = rcos(wt – j) = r cosj coswt + r sinj sinwt = z coswt + hsinwt

со случайными амплитудой  и фазой 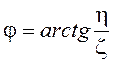. Для стационарности процесса x(t) в широком смысле достаточно, чтобы r и j были бы независимыми СВ и выполнялись бы условия

,

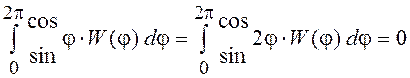т. е. ряд Фурье для ПВ фазы W(j), рассматриваемой как периодическая функция с периодом 2p, не должен содержать первых двух гармоник, иначе говоря, W(j) =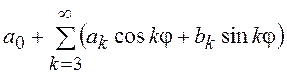. Естественно, должна быть обеспечена неотрицательность функции W(j). При W(j) = 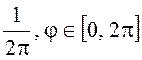 процесс будет стационарным в узком смысле [7]. С рассмотренной задачей связано каноническое представление СП, которое имеет вид