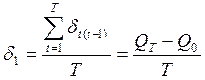Основные понятия экономической динамики. Характеристики экономического развития, страница 4

                           (9.9)

Второй способ ориентирован на сумму абсолютных уровней за период:

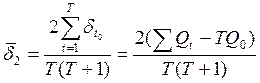    (9.10)

Величина  есть средняя арифметическая из последовательных цепных абсолютных приростов, взвешенная по их порядковым номерам, взятым в обратной последовательности[3]. Зная (или задав) значение , можно определить сумму значений интересующего показателя за T лет:

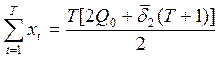                     (9.11)

Показатели  и  равны между собой, если последовательные абсолютные приросты постоянны (рост по линейному закону). При последовательном увеличении цепных абсолютных приростов >  и наоборот.

Второй показатель среднего абсолютного прироста имеет особое значение для характеристики динамики капитальных вложений, поскольку пятилетний план включает задание по объему капитальных вложений за пять лет. Сравнение показателей средних абсолютных и относительных приростов дается в табл. 9.4.

Таблица 9.4

Средние абсолютные приросты и средние темпы прироста капитальных вложений в народное хозяйство СССР (в сопоставимых ценах)

Средний темп роста. Задачам обобщенной оценки интенсивности экономического развития в наибольшей степени отвечают две модификации среднего темпа роста: среднийгеометрический и средний параболический (полиномиальный).

Первый показатель ориентирован на общий темп роста за период и представляет собой среднюю геометрическую из последовательных цепных темпов роста:

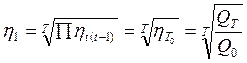(9.12)

Второй показатель ориентирован на сумму динамического ряда. Задача ставится следующим образом: определить темп роста, при котором исходя из начального уровня можно получить заданную сумму уровней за период (т.е. известны  и 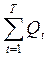). Тогда  определяется решением уравнения

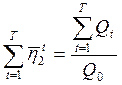           (9.13)

Величина  — это положительный корень данного уравнения (параболы T-го порядка). При Т> 2 уравнение не имеет аналитического решения. Поэтому вычисления  осуществляются приближенными методами, (в частности, методом Ньютона) или же по специальной таблице[4].

Средний темп  зависит только от крайних значений ряда, темп — от всех значений. Если цепные темпы роста постоянны в течение всего периода, то =.Если цепные темпы уменьшаются, то < .и наоборот.