Многоцелевая (векторная) оптимизация, страница 2

Условная субоптимизация. Пронумеруем частичные целевые функции так, что «главная» (непосредственно максимизируемая) целевая функция получает первый номер. Векторную функцию без первой частичной функции обозначим , а вектор фиксированных значений функций —. Имеем задачу:

f¹(X)→max, XÇ[X:(X)³](2.8)

По существу прикладные оптимизационные модели являются, как правило, моделями условной субоптимизации. Например, непосредственно максимизируется величина национального дохода или фонда потреб­ления, а уровни достижения других целей народного хозяйства (удовлетворение духовных потребностей, улучшение условий труда, повышение обороноспособности и т.д.) фиксируются в ограничениях модели.

В качестве максимизируемой в принципе может быть выбрана любая из частичных целевых функций и любая из них может быть ограничиваемой функцией. Таким образом, можно сформулировать и решить kзадач условной субоптимизации. Первоначально заданные уровни частичных целевых функций могут корректироваться в результате анализа субоптимальных решений.

Выбор компромиссного решения на основе условной субоптимизации может быть формализован. Пусть  — вектор субоптимальных значений целевых функций, Δ=(Δ_i) — вектор отклонений от ; — максимально допустимые отклонения от . Можно сформулировать такие задачи скалярной оптимизации:

f¹(X)→max, XÇ[X:(X)³≥Δ⁰]                       (2.9)

— максимизация одной частичной целевой функции при максимально допустимых отклонениях от оптимальных значений других целевых функций;

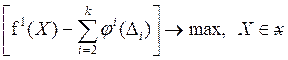               (2.10)

— максимизация разности одной частичной целевой функции и штрафной функции отклонений от субоптимальных значений других целевых функций, где φⁱ — монотонно возрастающая функция.

Легко видеть, что полная формализация выбора компромиссного решения требует принятия дополнительных допущений (о значениях  и вида функций φⁱ(Δ_i)).

Методика условной субоптимизации хорошо отражает специфику многоэтапного процесса построения народнохозяйственного плана, в котором трудно проводить грани между критериями оптимальности и ограничениями, а параметры всех условий последовательно уточняются по мере накопления необходимой информации и сужения области выбора оптимальных решений.

Скаляризация (свертка) векторного критерия оптимальности. Основными вопросами, возникающими при реализации данного подхода, являются учет приоритета (различной степени важности) частичных критериев оптимальности, нахождение разумных компромиссов между ними, сопоставление масштабов измерений различных критериев.

Рассмотрим некоторые приемы построения скалярной целевой функции на основе частичных целевых функций.

Выше отмечалась возможность использования функций F₁(X)= 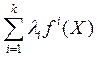 при выборе эффективных вариантов. Преимуществом такой скалярной функции является наглядная имитация влияния коэффициентов приоритета X, на выбор оптимальных решений. Недостатком данной функции является то, что она допускает резкую дифференциацию значений частичных целевых функций; например, возможно, что только одна функция f¹(X) будет положительной. Поэтому модель оптимизации со скалярной функцией

F₁(X)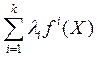

должна дополняться условиями, ограничивающими дифференциацию уровней частичных функций. При обосновании коэффициентов l_i - необходимо также учитывать масштабы изменений частичных функций.

Принцип «справедливого» компромисса при объединении нескольких критериев можно математически выразить в более сильной форме. Мы можем, в частности, считать справедливым такой компромисс, когда при сравнении вариантов решений относительное снижение по одним критериям не превосходит относительного повышения по другим. Такому условию отвечает функция

F₂(X)= 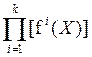                                    (2.11)

Например, варианты Х_А и X_B являются эквивалентными с точки зрения двух критериев f¹(X) и f²(X) если

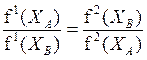
При использовании функции (2.11) допускается, что все частичные критерии одинаково важны. Различную степень важности частичных критери­ев можно учитывать в функции вида

F₃(X)= 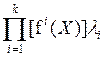                              (2.12)

В более развитом виде принцип справедливого компромисса учитывается посредством уравнивания уступок от субоптимальных значений - частичных целевых функций.

В практике моделирования довольно распространен принцип равномерной оптимизации. Идея его заключается в стремлении более или менее равномерно увеличивать степень достижения всех разнокачественных целей. При этом общей целью оптимизации является максимальное приближение к «идеальному» состоянию, задаваемому вектором .