15.4. Итеративное агрегирование
Принципиальным отличием методов итеративного агрегирования от других декомпозиционных подходов является наличие операторов агрегирования и дезагрегирования информационных потоков между задачами разных уровней. Каждый конкретный метод агрегирования характеризуется определенными правилами перехода от исходных показателей к агрегированным и наоборот. Простейшим правилом агрегирования является суммирование отдельных групп исходных (детализированных) показателей. Часто используются также взвешенные суммы (например, при переходе от натуральных к стоимостным показателям при фиксированных ценах) или средние величины.
Координирующая задача, получаемая посредством агрегирования, содержит меньшее число переменных, чем исходная. После нахождения решения координирующей задачи и его дезагрегации по заданным правилам строится решение (точное или приближенное) исходной задачи (метамодели).
Рассмотрим типичную постановку задачи согласования решений подсистем с использованием методов итеративного агрегирования. Пусть исходная задача имеет вид:
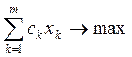
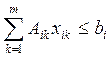 , i
= 1, …, n(15.8)
, i
= 1, …, n(15.8)
![]() , k
= 1, …, m
, k
= 1, …, m
Здесь ![]() , xk— векторы размерности mk, bi — вектор размерности ni, Aik — матрица размерности niх mk.
, xk— векторы размерности mk, bi — вектор размерности ni, Aik — матрица размерности niх mk.
Символами Mk и Niобозначим множества индексов компонент соответствующих векторов. Обозначим через L правый оператор агрегирования (агрегирование по столбцам), Г — левый оператор агрегирования (агрегирование по строкам) задачи (15.18).
Операторы
L
и Г являются в данном случае матрицами размерности 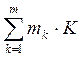 и
и 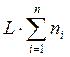 , где параметры К и Lзадают размерность
агрегированной задачи.
, где параметры К и Lзадают размерность
агрегированной задачи.
Внутренняя структура операторов L и Г зависит от типа объединения детализированных способов и условий в агрегированную номенклатуру. Для упрощения последующих рассуждений будем предполагать, что матрицы Aikзадачи (15.18) агрегируются в число (матрицы размерности 1 х 1). В этом случае агрегированная задача имеет размерность п х т, каждая k-я группа способов представима в ней одним обобщенным способом, каждая i-я группа условий агрегируется в одно ограничение.
С использованием операторов агрегирования L и Г исходная задача (15.18) "свертывается" в задачу меньшей размерности следующего вида:
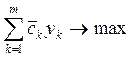
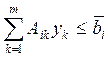 , i = 1, .., n (15.19)
, i = 1, .., n (15.19)
![]() , k
= 1, …, m
, k
= 1, …, m
Параметры
![]() ,
, ![]() ,
, ![]() , i=1, 2, …, n, k = 1, ..., mрассчитываются
следующим образом: с = сL,
, i=1, 2, …, n, k = 1, ..., mрассчитываются
следующим образом: с = сL, ![]() , А =
, А =![]() , где с, b, A — векторы коэффициентов
целевой функции, ограничений и матрица задачи (15.18).
, где с, b, A — векторы коэффициентов
целевой функции, ограничений и матрица задачи (15.18).
Между решениями задачи (15.18) и ее агрегированной версией (15.19) существует тесная взаимосвязь.
1. Пусть параметры
операторов агрегирования L = ![]() и Г =
и Г = ![]() определяются решением задачи (15.18) —
определяются решением задачи (15.18) — ![]() и двойственной к ней -
и двойственной к ней - ![]() :
: ![]() ,
, ![]() , k= 1, ..., m,
, k= 1, ..., m, ![]() ,
, ![]() , i = 1, …, n. Тогда оптимальные
решения агрегированных прямой и двойственной к ней задач
, i = 1, …, n. Тогда оптимальные
решения агрегированных прямой и двойственной к ней задач ![]() могут
принимать значения 1 или 0. При этом, если векторы
могут
принимать значения 1 или 0. При этом, если векторы ![]() имеют
хотя бы па одной ненулевой компоненте, то соответствующие
имеют
хотя бы па одной ненулевой компоненте, то соответствующие ![]() .
.
2. Если операторы агрегирования определяются через нормированные решения исходной задачи (15.18) и двойственной к ней
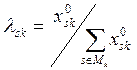 , s Î Mk , k = 1, …, m,
, s Î Mk , k = 1, …, m,
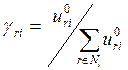 , r Î Ni
, i = 1, …,n,
, r Î Ni
, i = 1, …,n,
то справедливы следующие утверждения:
а) векторы ![]() ,
, ![]() с компонентами
с компонентами ![]() ,
, ![]() , k = 1,..., m, i= 1,..., nявляются решениями агрегированной задачи
(15.19) и двойственной к ней;
, k = 1,..., m, i= 1,..., nявляются решениями агрегированной задачи
(15.19) и двойственной к ней;
б) если, ![]() - прямое и двойственное решения агрегированной задачи (15.19), то векторы
- прямое и двойственное решения агрегированной задачи (15.19), то векторы ![]() ,
, ![]() , k = 1, …., т, i= 1, ..., n с компонентами, полученными дезагрегацией
решения у*, v*, x*= Ly*, u* = v*Г или
, k = 1, …., т, i= 1, ..., n с компонентами, полученными дезагрегацией
решения у*, v*, x*= Ly*, u* = v*Г или ![]() , s Î Mk, k = 1, …, m;
, s Î Mk, k = 1, …, m; ![]() , rÎNi, i = 1, …, nявляются решениями
исходной задачи (15.18) и двойственной к ней.
, rÎNi, i = 1, …, nявляются решениями
исходной задачи (15.18) и двойственной к ней.
Рассмотрим в качестве примера исходную задачу (15.16) размерности 2x2:
x1 ³ 0, x2 ³ 0
a11x1 + a12x2 £ b1
a21x1 + a22x2 £ b2
c1x1 + c2x2 ® max
С
помощью операторов агрегирования по столбцам L= (![]() ) и по строкам Г= (
) и по строкам Г= (![]() ) легко
построить агрегированную задачу размерности 1x1:
) легко
построить агрегированную задачу размерности 1x1:
y ³ 0
![]() (15.21)
(15.21)
![]()
где
![]() ,
, ![]()
![]()
Пусть x0 — (![]() ), u0 =
), u0 =![]() - оптимальные решения задачи
(15.20) и двойственной к ней и L0= (
- оптимальные решения задачи
(15.20) и двойственной к ней и L0= (![]() ), Г0 =
), Г0 = ![]() . Тогда из оптимальности x0, u0 и определения
параметров агрегированной задачи (15.21) следует, что
. Тогда из оптимальности x0, u0 и определения
параметров агрегированной задачи (15.21) следует, что
![]() ;
;
![]() (15.22)
(15.22)
Из соотношений (15.22) следует, что оптимальные решения агрегированной задачи и двойственной к ней равны 1.
Пусть компоненты операторов агрегирования L0 , G0 определяются нормированными оптимальными двойственными планами:
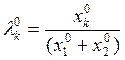 ; k
= 1, 2;
; k
= 1, 2;
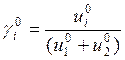 ;
i =1, 2.
;
i =1, 2.
Тогда
векторы y0 = ![]() и v0 =
и v0 = ![]() оптимальны
в агрегированной задаче (15.22) и двойственной
к ней.
оптимальны
в агрегированной задаче (15.22) и двойственной
к ней.
Действительно, допустимость очевидна:
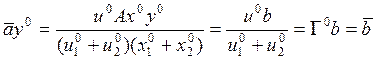 ;
;
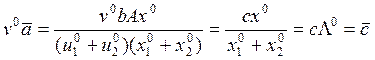 ;
;
![]() .
.
Если
решение агрегированной задачи существует, то оно равно ![]() .
С другой стороны, согласно утверждению 2а,
.
С другой стороны, согласно утверждению 2а,
![]() - также решение (15.21). Следовательно,
- также решение (15.21). Следовательно, ![]() и
и ![]() допустимы в исходной задаче
допустимы в исходной задаче
Отмеченные
соотношения между решениями исходной задачи и ее агрегированного аналога дают возможность
построить процесс согласования решений. Как и в других декомпозиционных схемах,
исходная задача
(15.18) разбивается на локальные задачи подсистем и координирующую задачу.
Последняя обычно представляет агрегированный аналог (уменьшенную копию)
исходной задачи. Композиция локально-оптимальных планов подсистем, полученных на очередной итерации, задает
очередное приближенное решение задачи
(15.18). По соотношению между решениями
агрегированной задачи ![]() ,
, ![]() локальных
задач
локальных
задач ![]() ,
, ![]() точнее, по разнице
точнее, по разнице
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.